
Question Number 213047 by hardmath last updated on 29/Oct/24
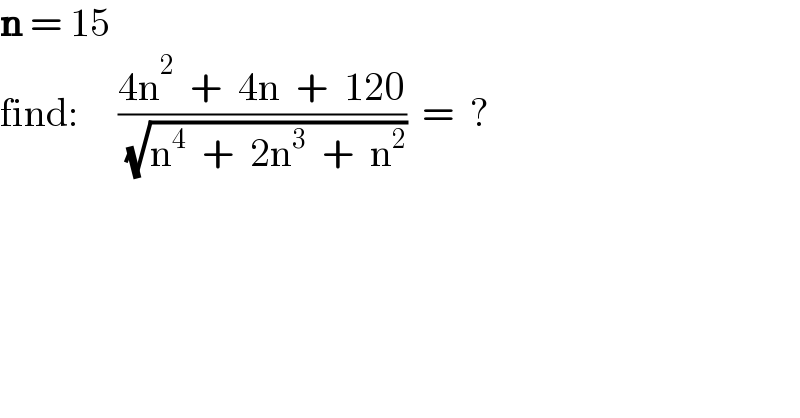
$$\boldsymbol{\mathrm{n}}\:=\:\mathrm{15} \\ $$$$\mathrm{find}:\:\:\:\:\:\frac{\mathrm{4n}^{\mathrm{2}} \:\:+\:\:\mathrm{4n}\:\:+\:\:\mathrm{120}}{\:\sqrt{\mathrm{n}^{\mathrm{4}} \:\:+\:\:\mathrm{2n}^{\mathrm{3}} \:\:+\:\:\mathrm{n}^{\mathrm{2}} }}\:\:=\:\:? \\ $$
Answered by mehdee7396 last updated on 29/Oct/24

$$\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{119}}{{n}\left({n}+\mathrm{1}\right)}=\mathrm{4}.\mathrm{5} \\ $$
Answered by MrGaster last updated on 29/Oct/24

$$\frac{\mathrm{4}\centerdot\mathrm{15}^{\mathrm{2}} +\mathrm{4}\centerdot\mathrm{15}+\mathrm{120}}{\:\sqrt{\mathrm{15}^{\mathrm{4}} +\mathrm{2}\centerdot\mathrm{15}^{\mathrm{3}} +\mathrm{15}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{4}\centerdot\mathrm{225}+\mathrm{60}+\mathrm{120}}{\:\sqrt{\mathrm{50625}+\mathrm{6750}+\mathrm{225}}} \\ $$$$\frac{\mathrm{900}+\mathrm{60}+\mathrm{120}}{\:\sqrt{\mathrm{57600}}} \\ $$$$\frac{\mathrm{1080}}{\mathrm{240}} \\ $$$$=\mathrm{4}.\mathrm{5} \\ $$
Commented by hardmath last updated on 03/Nov/24
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professors} \\ $$
