
Question Number 111466 by Dwaipayan Shikari last updated on 03/Sep/20

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{{n}} }{{n}!} \\ $$
Commented by Her_Majesty last updated on 03/Sep/20
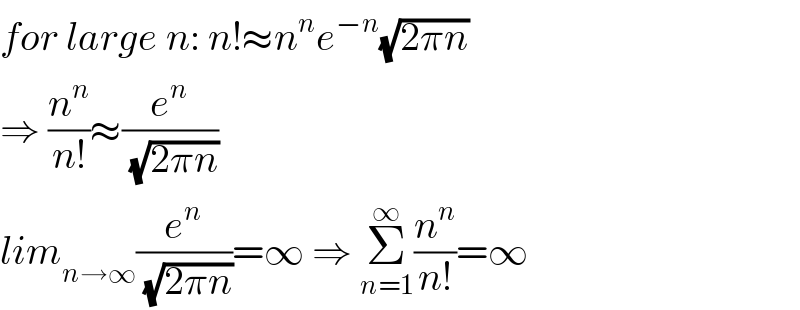
$${for}\:{large}\:{n}:\:{n}!\approx{n}^{{n}} {e}^{−{n}} \sqrt{\mathrm{2}\pi{n}} \\ $$$$\Rightarrow\:\frac{{n}^{{n}} }{{n}!}\approx\frac{{e}^{{n}} }{\:\sqrt{\mathrm{2}\pi{n}}} \\ $$$${lim}_{{n}\rightarrow\infty} \frac{{e}^{{n}} }{\:\sqrt{\mathrm{2}\pi{n}}}=\infty\:\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{{n}} }{{n}!}=\infty \\ $$
Commented by Her_Majesty last updated on 03/Sep/20

$$...{but}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}!}{{n}^{{n}} }\:{exists} \\ $$
Answered by malwaan last updated on 03/Sep/20
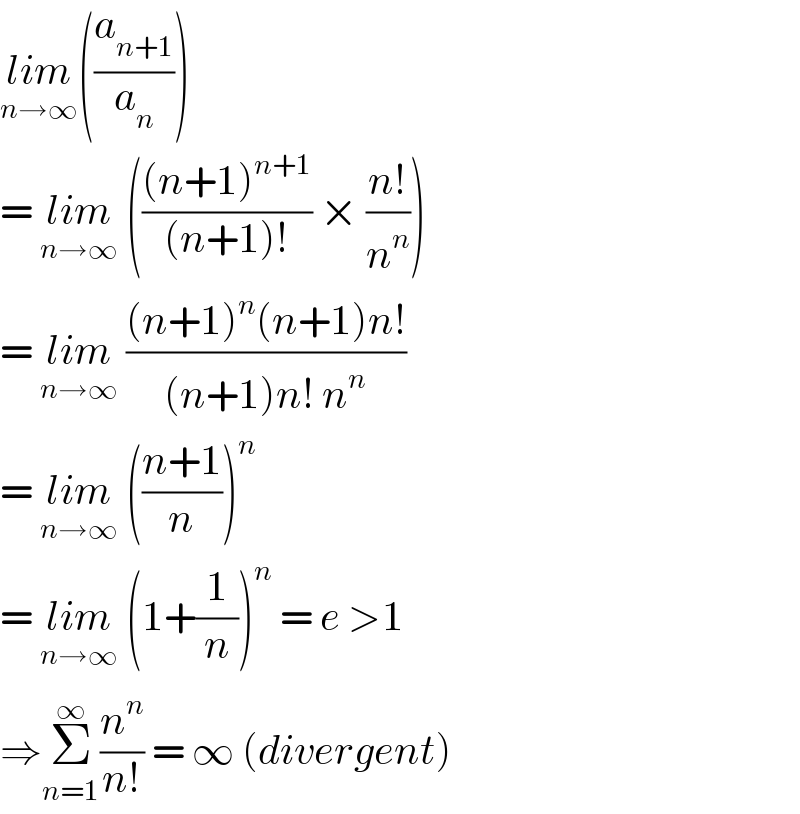
$$\underset{{n}\rightarrow\infty} {{lim}}\left(\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }\right) \\ $$$$=\:\underset{{n}\rightarrow\infty} {{lim}}\:\left(\frac{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}\:×\:\frac{{n}!}{{n}^{{n}} }\right) \\ $$$$=\:\underset{{n}\rightarrow\infty} {{lim}}\:\frac{\left({n}+\mathrm{1}\right)^{{n}} \left({n}+\mathrm{1}\right){n}!}{\left({n}+\mathrm{1}\right){n}!\:{n}^{{n}} } \\ $$$$=\:\underset{{n}\rightarrow\infty} {{lim}}\:\left(\frac{{n}+\mathrm{1}}{{n}}\right)^{{n}} \\ $$$$=\:\underset{{n}\rightarrow\infty} {{lim}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \:=\:{e}\:>\mathrm{1} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\Sigma}}\:\frac{{n}^{{n}} }{{n}!}\:=\:\infty\:\left({divergent}\right) \\ $$
