Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 192590 by York12 last updated on 22/May/23

Σ_(n=1) ^∞ Σ_(m=1) ^∞ [((m^2 n)/(3^m (3^n .m+3^m .n)))]=λ find λ.

$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{{m}^{\mathrm{2}} {n}}{\mathrm{3}^{{m}} \left(\mathrm{3}^{{n}} .{m}+\mathrm{3}^{{m}} .{n}\right)}\right]=\lambda\: \\ $$$${find}\:\lambda. \\ $$$$ \\ $$

Answered by witcher3 last updated on 24/May/23

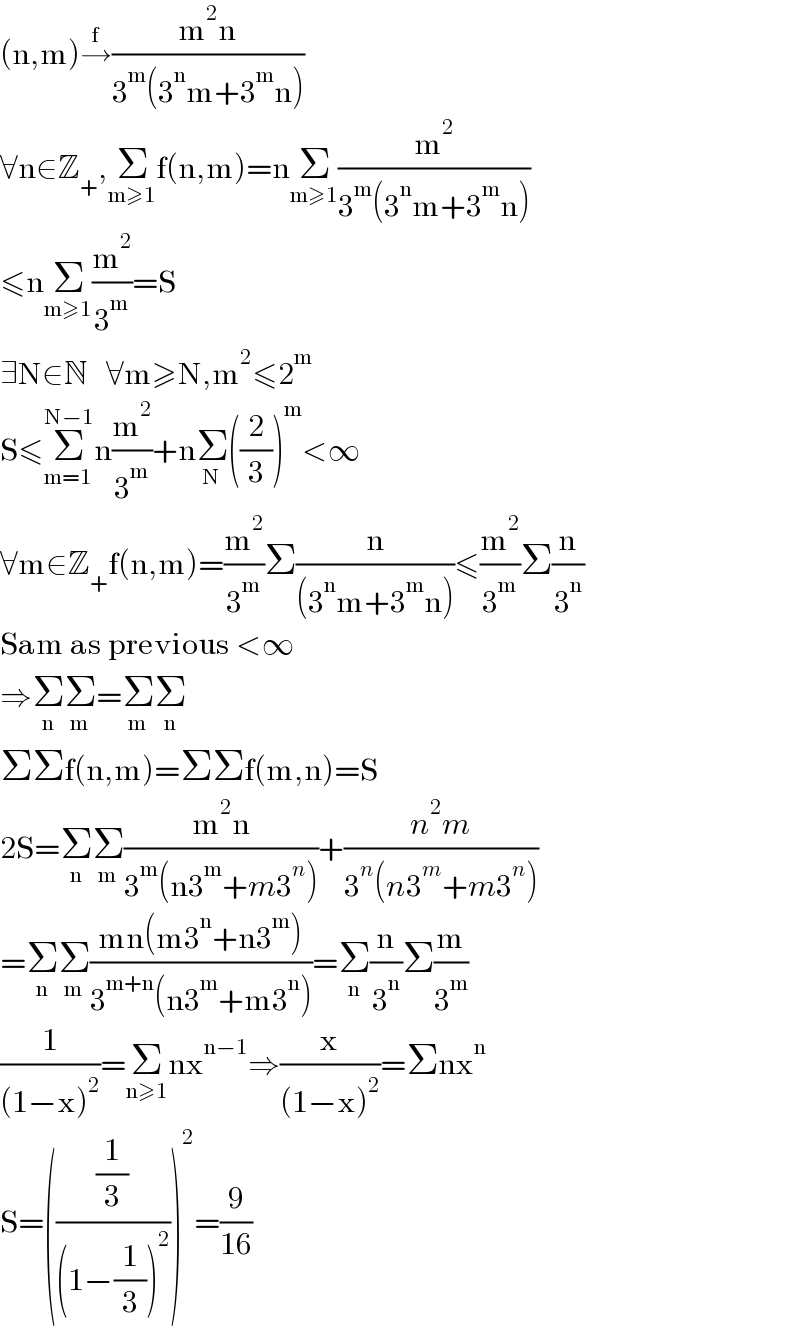
(n,m)→^f ((m^2 n)/(3^m (3^n m+3^m n))) ∀n∈Z_+ ,Σ_(m≥1) f(n,m)=nΣ_(m≥1) (m^2 /(3^m (3^n m+3^m n))) ≤nΣ_(m≥1) (m^2 /3^m )=S ∃N∈N ∀m≥N,m^2 ≤2^m S≤Σ_(m=1) ^(N−1) n(m^2 /3^m )+nΣ_N ((2/3))^m <∞ ∀m∈Z_+ f(n,m)=(m^2 /3^m )Σ(n/((3^n m+3^m n)))≤(m^2 /3^m )Σ(n/3^n ) Sam as previous <∞ ⇒Σ_n Σ_m =Σ_m Σ_n ΣΣf(n,m)=ΣΣf(m,n)=S 2S=Σ_n Σ_m ((m^2 n)/(3^m (n3^m +m3^n )))+((n^2 m)/(3^n (n3^m +m3^n ))) =Σ_n Σ_m ((mn(m3^n +n3^m ))/(3^(m+n) (n3^m +m3^n )))=Σ_n (n/3^n )Σ(m/3^m ) (1/((1−x)^2 ))=Σ_(n≥1) nx^(n−1) ⇒(x/((1−x)^2 ))=Σnx^n S=(((1/3)/((1−(1/3))^2 )))^2 =(9/(16))

$$\left(\mathrm{n},\mathrm{m}\right)\overset{\mathrm{f}} {\rightarrow}\frac{\mathrm{m}^{\mathrm{2}} \mathrm{n}}{\mathrm{3}^{\mathrm{m}} \left(\mathrm{3}^{\mathrm{n}} \mathrm{m}+\mathrm{3}^{\mathrm{m}} \mathrm{n}\right)} \\ $$$$\forall\mathrm{n}\in\mathbb{Z}_{+} ,\underset{\mathrm{m}\geqslant\mathrm{1}} {\sum}\mathrm{f}\left(\mathrm{n},\mathrm{m}\right)=\mathrm{n}\underset{\mathrm{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{m}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{m}} \left(\mathrm{3}^{\mathrm{n}} \mathrm{m}+\mathrm{3}^{\mathrm{m}} \mathrm{n}\right)} \\ $$$$\leqslant\mathrm{n}\underset{\mathrm{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{m}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{m}} }=\mathrm{S} \\ $$$$\exists\mathrm{N}\in\mathbb{N}\:\:\:\forall\mathrm{m}\geqslant\mathrm{N},\mathrm{m}^{\mathrm{2}} \leqslant\mathrm{2}^{\mathrm{m}} \\ $$$$\mathrm{S}\leqslant\underset{\mathrm{m}=\mathrm{1}} {\overset{\mathrm{N}−\mathrm{1}} {\sum}}\mathrm{n}\frac{\mathrm{m}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{m}} }+\mathrm{n}\underset{\mathrm{N}} {\sum}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{m}} <\infty \\ $$$$\forall\mathrm{m}\in\mathbb{Z}_{+} \mathrm{f}\left(\mathrm{n},\mathrm{m}\right)=\frac{\mathrm{m}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{m}} }\Sigma\frac{\mathrm{n}}{\left(\mathrm{3}^{\mathrm{n}} \mathrm{m}+\mathrm{3}^{\mathrm{m}} \mathrm{n}\right)}\leqslant\frac{\mathrm{m}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{m}} }\Sigma\frac{\mathrm{n}}{\mathrm{3}^{\mathrm{n}} } \\ $$$$\mathrm{Sam}\:\mathrm{as}\:\mathrm{previous}\:<\infty \\ $$$$\Rightarrow\underset{\mathrm{n}} {\sum}\underset{\mathrm{m}} {\sum}=\underset{\mathrm{m}} {\sum}\underset{\mathrm{n}} {\sum} \\ $$$$\Sigma\Sigma\mathrm{f}\left(\mathrm{n},\mathrm{m}\right)=\Sigma\Sigma\mathrm{f}\left(\mathrm{m},\mathrm{n}\right)=\mathrm{S} \\ $$$$\mathrm{2S}=\underset{\mathrm{n}} {\sum}\underset{\mathrm{m}} {\sum}\frac{\mathrm{m}^{\mathrm{2}} \mathrm{n}}{\mathrm{3}^{\mathrm{m}} \left(\mathrm{n3}^{\mathrm{m}} +{m}\mathrm{3}^{{n}} \right)}+\frac{{n}^{\mathrm{2}} {m}}{\mathrm{3}^{{n}} \left({n}\mathrm{3}^{{m}} +{m}\mathrm{3}^{{n}} \right)} \\ $$$$=\underset{\mathrm{n}} {\sum}\underset{\mathrm{m}} {\sum}\frac{\mathrm{mn}\left(\mathrm{m3}^{\mathrm{n}} +\mathrm{n3}^{\mathrm{m}} \right)}{\mathrm{3}^{\mathrm{m}+\mathrm{n}} \left(\mathrm{n3}^{\mathrm{m}} +\mathrm{m3}^{\mathrm{n}} \right)}=\underset{\mathrm{n}} {\sum}\frac{\mathrm{n}}{\mathrm{3}^{\mathrm{n}} }\Sigma\frac{\mathrm{m}}{\mathrm{3}^{\mathrm{m}} } \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }=\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \Rightarrow\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }=\Sigma\mathrm{nx}^{\mathrm{n}} \\ $$$$\mathrm{S}=\left(\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\right)^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{16}} \\ $$

Commented by York12 last updated on 24/May/23

Great ! what book do you recommend for algebra

$${Great}\:! \\ $$$${what}\:{book}\:{do}\:{you}\:{recommend}\:{for}\:{algebra} \\ $$

Commented by witcher3 last updated on 24/May/23

hello sir sorry for last times not responding i have not telegram book 1 introduce to matrix and linear algebra 2) for calculus almost Impossible sum and integrals contein hards problems !

$$\mathrm{hello}\:\mathrm{sir}\:\mathrm{sorry}\:\mathrm{for}\:\mathrm{last}\:\mathrm{times} \\ $$$$\mathrm{not}\:\mathrm{responding}\:\mathrm{i}\:\mathrm{have}\:\mathrm{not}\:\mathrm{telegram} \\ $$$$\mathrm{book}\:\mathrm{1}\:\mathrm{introduce}\:\mathrm{to}\:\mathrm{matrix}\:\mathrm{and}\:\mathrm{linear}\:\mathrm{algebra} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{for}\:\mathrm{calculus} \\ $$$$\mathrm{almost}\:\mathrm{Impossible}\:\mathrm{sum}\:\mathrm{and}\:\mathrm{integrals} \\ $$$$\mathrm{contein}\:\mathrm{hards}\:\mathrm{problems}\:!\: \\ $$$$ \\ $$

Commented by York12 last updated on 24/May/23

thanks so much , No problem

$${thanks}\:{so}\:{much}\:,\:{No}\:{problem} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com