
Question Number 104471 by Dwaipayan Shikari last updated on 21/Jul/20

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{n}} {n}!}{{n}^{{n}} } \\ $$
Answered by MAB last updated on 21/Jul/20
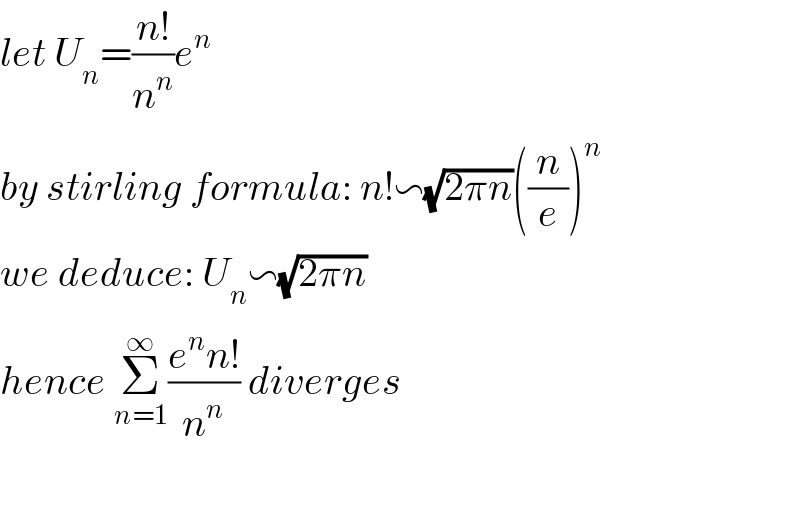
$${let}\:{U}_{{n}} =\frac{{n}!}{{n}^{{n}} }{e}^{{n}} \\ $$$${by}\:{stirling}\:{formula}:\:{n}!\backsim\sqrt{\mathrm{2}\pi{n}}\left(\frac{{n}}{{e}}\right)^{{n}} \\ $$$${we}\:{deduce}:\:{U}_{{n}} \backsim\sqrt{\mathrm{2}\pi{n}} \\ $$$${hence}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{n}} {n}!}{{n}^{{n}} }\:{diverges} \\ $$$$ \\ $$
