
Question Number 166254 by mnjuly1970 last updated on 16/Feb/22
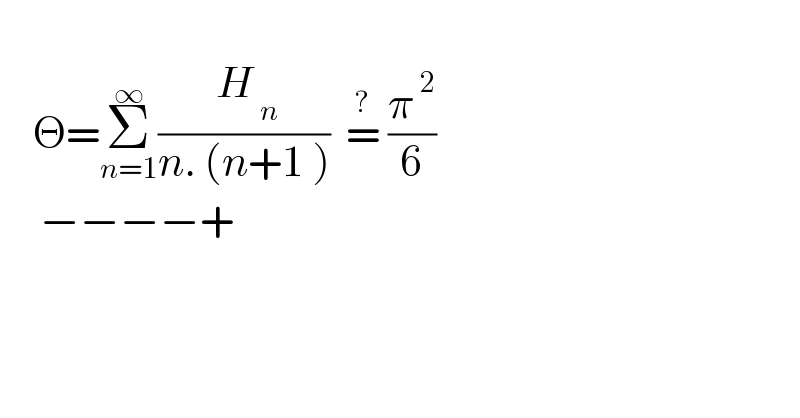
$$ \\ $$$$\:\:\:\:\Theta=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:{H}_{\:{n}} }{{n}.\:\left({n}+\mathrm{1}\:\right)}\:\:\overset{?} {=}\:\frac{\pi^{\:\mathrm{2}} }{\mathrm{6}} \\ $$$$\:\:\:\:\:−−−−+ \\ $$
Answered by Kamel_Ben last updated on 16/Feb/22
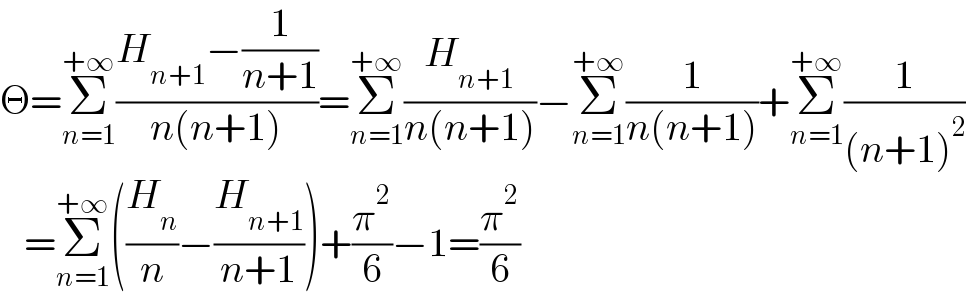
$$\Theta=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{H}_{{n}+\mathrm{1}} −\frac{\mathrm{1}}{{n}+\mathrm{1}}}{{n}\left({n}+\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{H}_{{n}+\mathrm{1}} }{{n}\left({n}+\mathrm{1}\right)}−\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}+\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\left(\frac{{H}_{{n}} }{{n}}−\frac{{H}_{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
