Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 17767 by Joel577 last updated on 10/Jul/17

Σ_(n = 1) ^(30) (n^2 + 1) = (A) Σ_(n = 1) ^(15) (2n^2 + 30n + 224) (B) Σ_(n = 1) ^(15) (2n^2 + 30n + 225) (C) Σ_(n = 1) ^(15) (2n^2 + 30n + 226) (D) Σ_(n = 1) ^(15) (2n^2 + 30n + 227) (E) Σ_(n = 1) ^(15) (2n^2 + 30n + 228)

$$\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{30}} {\sum}}\left({n}^{\mathrm{2}} \:+\:\mathrm{1}\right)\:=\: \\ $$$$\left(\mathrm{A}\right)\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(\mathrm{2}{n}^{\mathrm{2}} \:+\:\mathrm{30}{n}\:+\:\mathrm{224}\right) \\ $$$$\left(\mathrm{B}\right)\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(\mathrm{2}{n}^{\mathrm{2}} \:+\:\mathrm{30}{n}\:+\:\mathrm{225}\right) \\ $$$$\left(\mathrm{C}\right)\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(\mathrm{2}{n}^{\mathrm{2}} \:+\:\mathrm{30}{n}\:+\:\mathrm{226}\right) \\ $$$$\left(\mathrm{D}\right)\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(\mathrm{2}{n}^{\mathrm{2}} \:+\:\mathrm{30}{n}\:+\:\mathrm{227}\right) \\ $$$$\left(\mathrm{E}\right)\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{15}} {\sum}}\left(\mathrm{2}{n}^{\mathrm{2}} \:+\:\mathrm{30}{n}\:+\:\mathrm{228}\right) \\ $$

Answered by Tinkutara last updated on 11/Jul/17

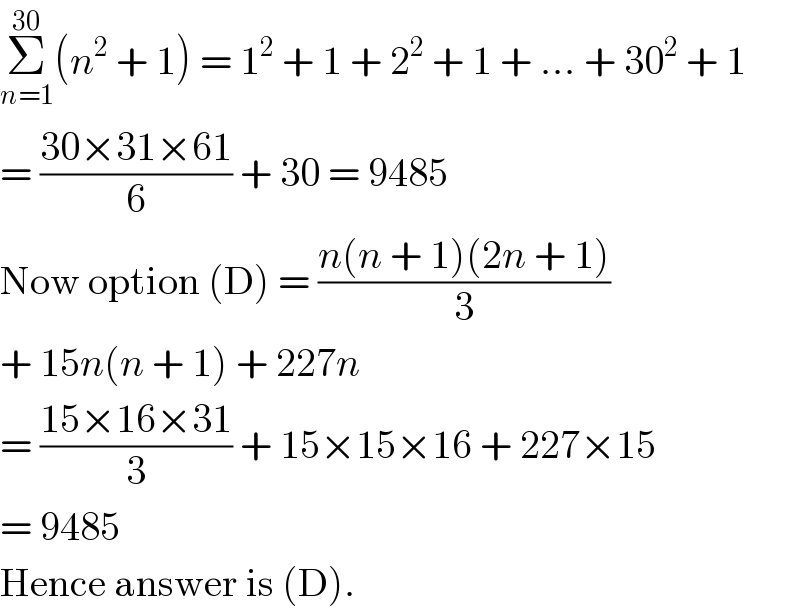
Σ_(n=1) ^(30) (n^2 + 1) = 1^2 + 1 + 2^2 + 1 + ... + 30^2 + 1 = ((30×31×61)/6) + 30 = 9485 Now option (D) = ((n(n + 1)(2n + 1))/3) + 15n(n + 1) + 227n = ((15×16×31)/3) + 15×15×16 + 227×15 = 9485 Hence answer is (D).

$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{30}} {\sum}}\left({n}^{\mathrm{2}} \:+\:\mathrm{1}\right)\:=\:\mathrm{1}^{\mathrm{2}} \:+\:\mathrm{1}\:+\:\mathrm{2}^{\mathrm{2}} \:+\:\mathrm{1}\:+\:...\:+\:\mathrm{30}^{\mathrm{2}} \:+\:\mathrm{1} \\ $$$$=\:\frac{\mathrm{30}×\mathrm{31}×\mathrm{61}}{\mathrm{6}}\:+\:\mathrm{30}\:=\:\mathrm{9485} \\ $$$$\mathrm{Now}\:\mathrm{option}\:\left(\mathrm{D}\right)\:=\:\frac{{n}\left({n}\:+\:\mathrm{1}\right)\left(\mathrm{2}{n}\:+\:\mathrm{1}\right)}{\mathrm{3}} \\ $$$$+\:\mathrm{15}{n}\left({n}\:+\:\mathrm{1}\right)\:+\:\mathrm{227}{n} \\ $$$$=\:\frac{\mathrm{15}×\mathrm{16}×\mathrm{31}}{\mathrm{3}}\:+\:\mathrm{15}×\mathrm{15}×\mathrm{16}\:+\:\mathrm{227}×\mathrm{15} \\ $$$$=\:\mathrm{9485} \\ $$$$\mathrm{Hence}\:\mathrm{answer}\:\mathrm{is}\:\left(\mathrm{D}\right). \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com