
Question Number 159775 by Ghaniy last updated on 22/Nov/21
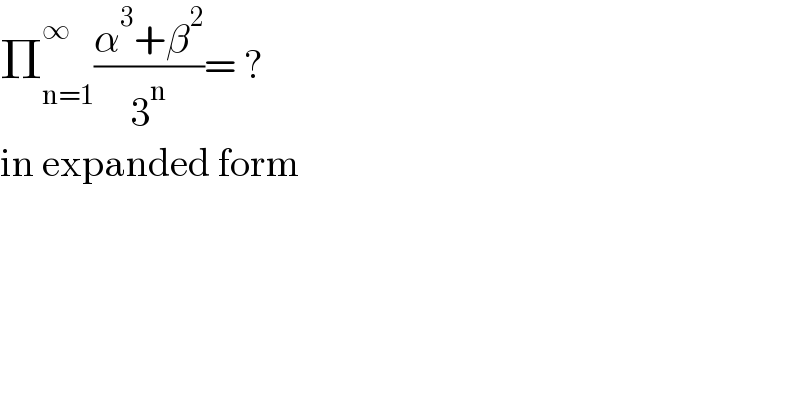
$$\prod_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\alpha^{\mathrm{3}} +\beta^{\mathrm{2}} }{\mathrm{3}^{\mathrm{n}} }=\:? \\ $$$$\mathrm{in}\:\mathrm{expanded}\:\mathrm{form} \\ $$
Answered by Canebulok last updated on 21/Nov/21

$$\: \\ $$$$\:\boldsymbol{\mathrm{Solution}}: \\ $$$$\: \\ $$$$\:\left(\mathrm{x}^{\mathrm{3}} +\pi^{\mathrm{2}} \right)\centerdot\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{100}} {\prod}}\:\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{n}} }\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{100}} {\prod}}\:\frac{\mathrm{x}^{\mathrm{3}} +\pi^{\mathrm{2}} }{\mathrm{4}^{\mathrm{n}} } \\ $$$$\: \\ $$$$\:\therefore \\ $$$$\:\left(\mathrm{x}^{\mathrm{3}} +\pi^{\mathrm{2}} \right)\centerdot\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{100}} {\prod}}\:\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{n}} }\:=\:\frac{\mathrm{x}^{\mathrm{3}} +\pi^{\mathrm{2}} }{\mathrm{4}^{\left(\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\:\mathrm{n}\right)} }\:=\:\frac{\mathrm{x}^{\mathrm{3}} +\pi^{\mathrm{2}} }{\mathrm{4}^{\mathrm{5050}} } \\ $$$$\: \\ $$$$\: \\ $$
Commented by Ghaniy last updated on 22/Nov/21
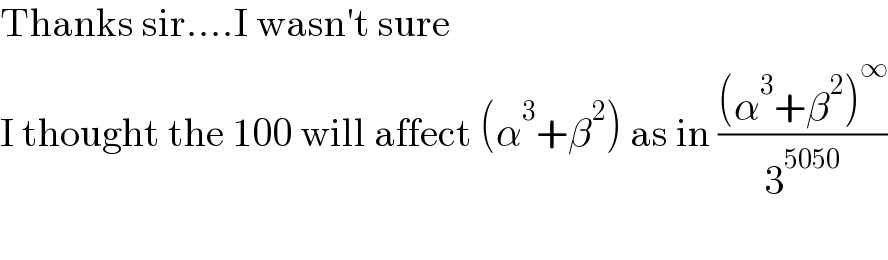
$$\mathrm{Thanks}\:\mathrm{sir}....\mathrm{I}\:\mathrm{wasn}'\mathrm{t}\:\mathrm{sure}\: \\ $$$$\mathrm{I}\:\mathrm{thought}\:\mathrm{the}\:\mathrm{100}\:\mathrm{will}\:\mathrm{affect}\:\left(\alpha^{\mathrm{3}} +\beta^{\mathrm{2}} \right)\:\mathrm{as}\:\mathrm{in}\:\frac{\left(\alpha^{\mathrm{3}} +\beta^{\mathrm{2}} \right)^{\infty} }{\mathrm{3}^{\mathrm{5050}} } \\ $$$$ \\ $$
