
Question Number 139560 by Dwaipayan Shikari last updated on 28/Apr/21
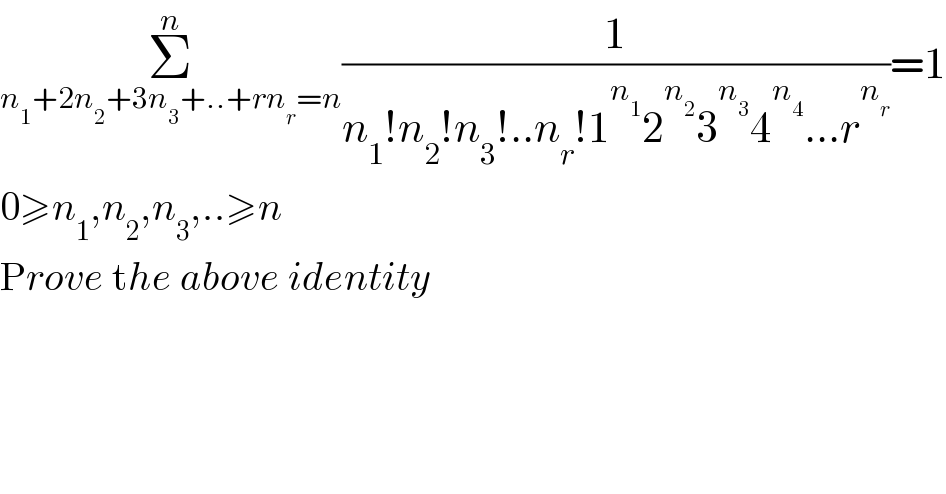
$$\underset{{n}_{\mathrm{1}} +\mathrm{2}{n}_{\mathrm{2}} +\mathrm{3}{n}_{\mathrm{3}} +..+{rn}_{{r}} ={n}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}_{\mathrm{1}} !{n}_{\mathrm{2}} !{n}_{\mathrm{3}} !..{n}_{{r}} !\mathrm{1}^{{n}_{\mathrm{1}} } \mathrm{2}^{{n}_{\mathrm{2}} } \mathrm{3}^{{n}_{\mathrm{3}} } \mathrm{4}^{{n}_{\mathrm{4}} } ...{r}^{{n}_{{r}} } }=\mathrm{1} \\ $$$$\mathrm{0}\geqslant{n}_{\mathrm{1}} ,{n}_{\mathrm{2}} ,{n}_{\mathrm{3}} ,..\geqslant{n} \\ $$$$\mathrm{P}{rove}\:\mathrm{t}{he}\:{above}\:{identity} \\ $$
