
Question Number 131825 by liberty last updated on 09/Feb/21
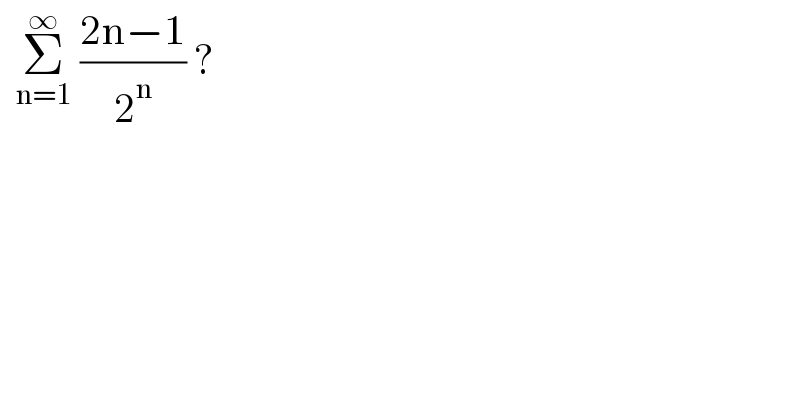
$$\:\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2n}−\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\:? \\ $$
Answered by mr W last updated on 09/Feb/21
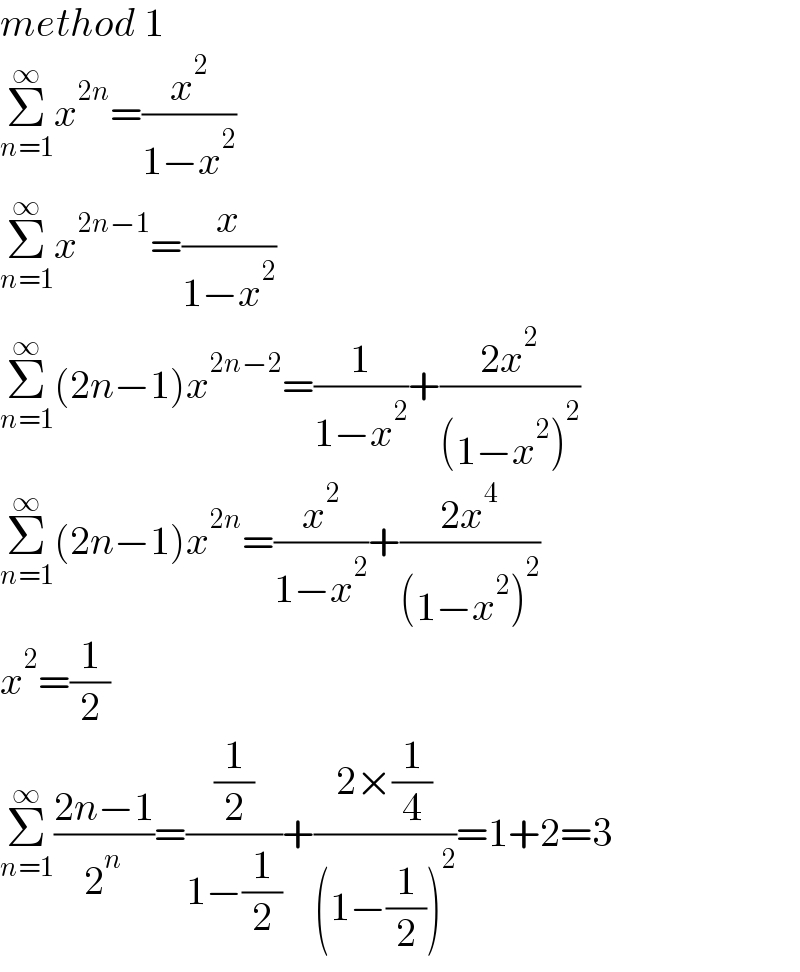
$${method}\:\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{\mathrm{2}{n}} =\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{\mathrm{2}{n}−\mathrm{1}} =\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\mathrm{2}{n}−\mathrm{1}\right){x}^{\mathrm{2}{n}−\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\mathrm{2}{n}−\mathrm{1}\right){x}^{\mathrm{2}{n}} =\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{\mathrm{2}{x}^{\mathrm{4}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}^{{n}} }=\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}+\frac{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{1}+\mathrm{2}=\mathrm{3} \\ $$
Commented by liberty last updated on 09/Feb/21

$$\mathrm{cool}... \\ $$
Commented by mr W last updated on 09/Feb/21
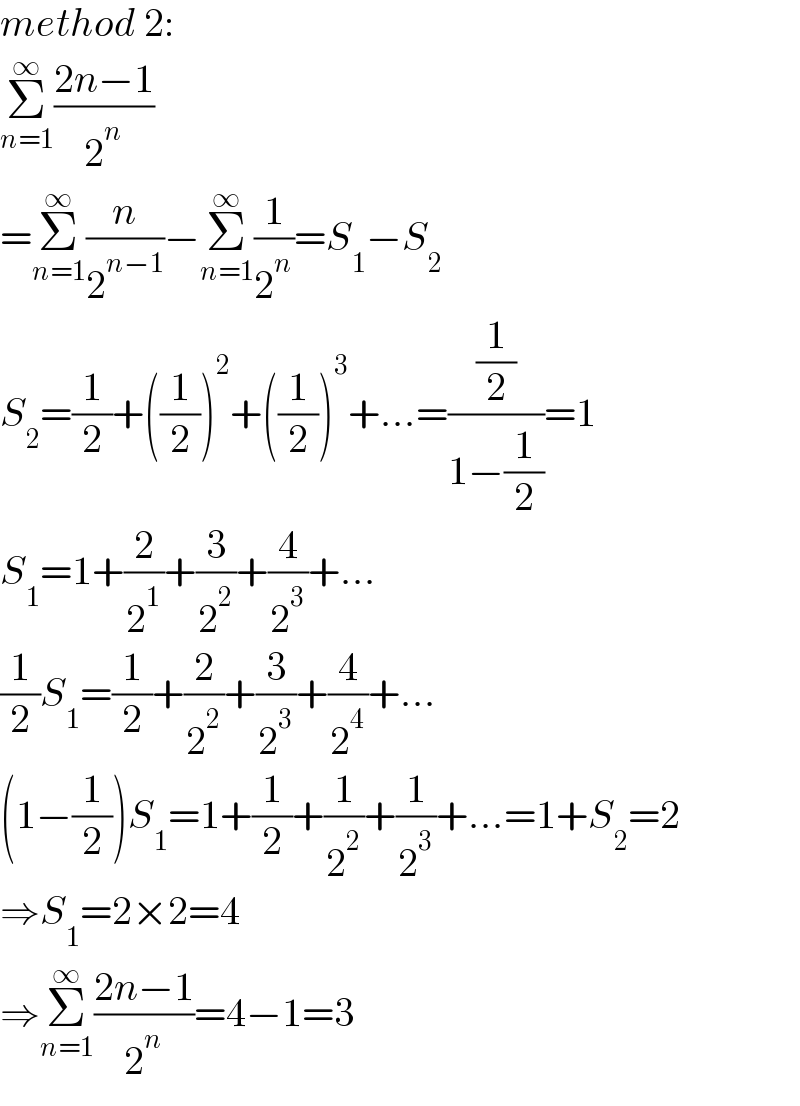
$${method}\:\mathrm{2}: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{\mathrm{2}^{{n}−\mathrm{1}} }−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} }={S}_{\mathrm{1}} −{S}_{\mathrm{2}} \\ $$$${S}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} +...=\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{1} \\ $$$${S}_{\mathrm{1}} =\mathrm{1}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{3}} }+... \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{S}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{2}^{\mathrm{4}} }+... \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right){S}_{\mathrm{1}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+...=\mathrm{1}+{S}_{\mathrm{2}} =\mathrm{2} \\ $$$$\Rightarrow{S}_{\mathrm{1}} =\mathrm{2}×\mathrm{2}=\mathrm{4} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}^{{n}} }=\mathrm{4}−\mathrm{1}=\mathrm{3} \\ $$
Answered by Dwaipayan Shikari last updated on 09/Feb/21
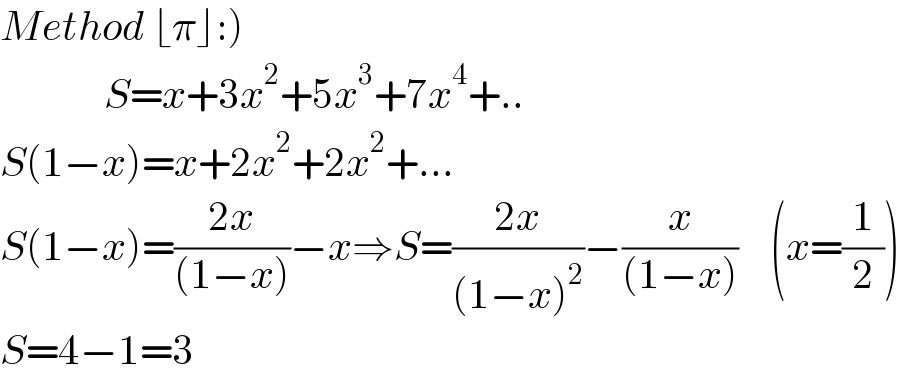
$$\left.{Method}\:\lfloor\pi\rfloor:\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{S}={x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{5}{x}^{\mathrm{3}} +\mathrm{7}{x}^{\mathrm{4}} +.. \\ $$$${S}\left(\mathrm{1}−{x}\right)={x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} +... \\ $$$${S}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)}−{x}\Rightarrow{S}=\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }−\frac{{x}}{\left(\mathrm{1}−{x}\right)}\:\:\:\:\left({x}=\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${S}=\mathrm{4}−\mathrm{1}=\mathrm{3} \\ $$
