
Question Number 108825 by ajfour last updated on 19/Aug/20
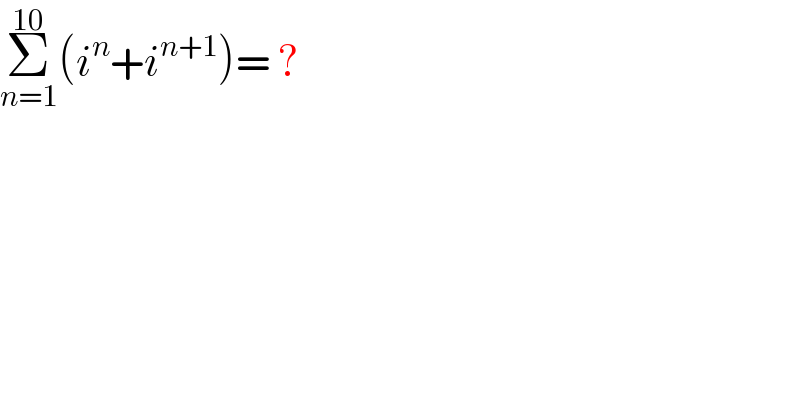
$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}\left({i}^{{n}} +{i}^{{n}+\mathrm{1}} \right)=\:? \\ $$
Commented by ajfour last updated on 19/Aug/20
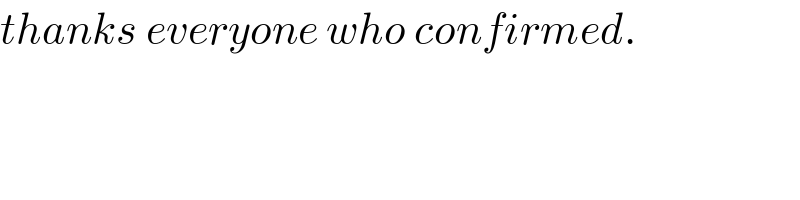
$${thanks}\:{everyone}\:{who}\:{confirmed}. \\ $$
Answered by john santu last updated on 19/Aug/20
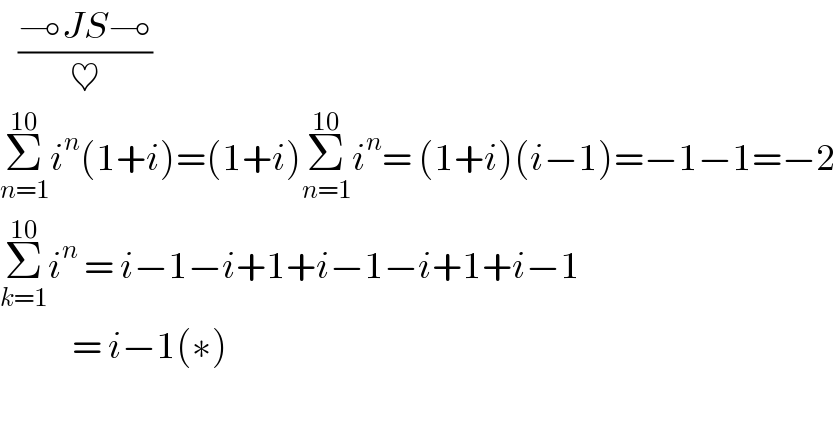
$$\:\:\:\frac{\multimap{JS}\multimap}{\heartsuit} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{i}^{{n}} \left(\mathrm{1}+{i}\right)=\left(\mathrm{1}+{i}\right)\underset{{n}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{i}^{{n}} =\:\left(\mathrm{1}+{i}\right)\left({i}−\mathrm{1}\right)=−\mathrm{1}−\mathrm{1}=−\mathrm{2} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{i}^{{n}} \:=\:{i}−\mathrm{1}−{i}+\mathrm{1}+{i}−\mathrm{1}−{i}+\mathrm{1}+{i}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:{i}−\mathrm{1}\left(\ast\right) \\ $$$$ \\ $$
Commented by ajfour last updated on 19/Aug/20
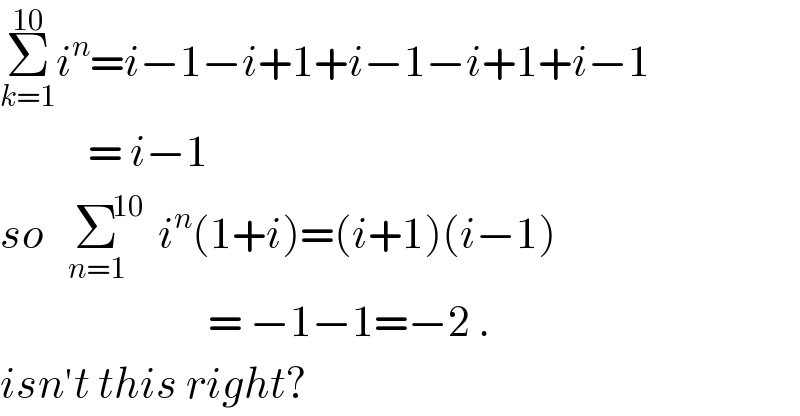
$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{10}} {\sum}}{i}^{{n}} ={i}−\mathrm{1}−{i}+\mathrm{1}+{i}−\mathrm{1}−{i}+\mathrm{1}+{i}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:{i}−\mathrm{1} \\ $$$${so}\:\:\:\underset{{n}=\mathrm{1}} {\sum}^{\mathrm{10}} {i}^{{n}} \left(\mathrm{1}+{i}\right)=\left({i}+\mathrm{1}\right)\left({i}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{1}−\mathrm{1}=−\mathrm{2}\:. \\ $$$${isn}'{t}\:{this}\:{right}? \\ $$
Commented by bemath last updated on 19/Aug/20

$${yes} \\ $$
Commented by john santu last updated on 19/Aug/20

$${yes} \\ $$
Answered by Dwaipayan Shikari last updated on 19/Aug/20
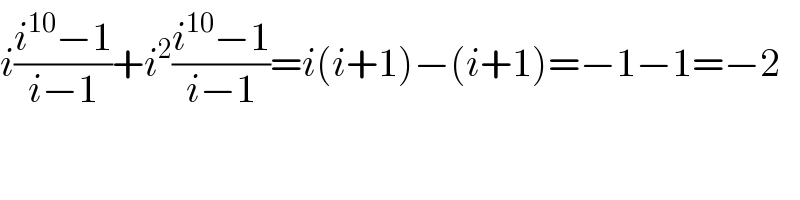
$${i}\frac{{i}^{\mathrm{10}} −\mathrm{1}}{{i}−\mathrm{1}}+{i}^{\mathrm{2}} \frac{{i}^{\mathrm{10}} −\mathrm{1}}{{i}−\mathrm{1}}={i}\left({i}+\mathrm{1}\right)−\left({i}+\mathrm{1}\right)=−\mathrm{1}−\mathrm{1}=−\mathrm{2} \\ $$
