Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 214302 by universe last updated on 04/Dec/24

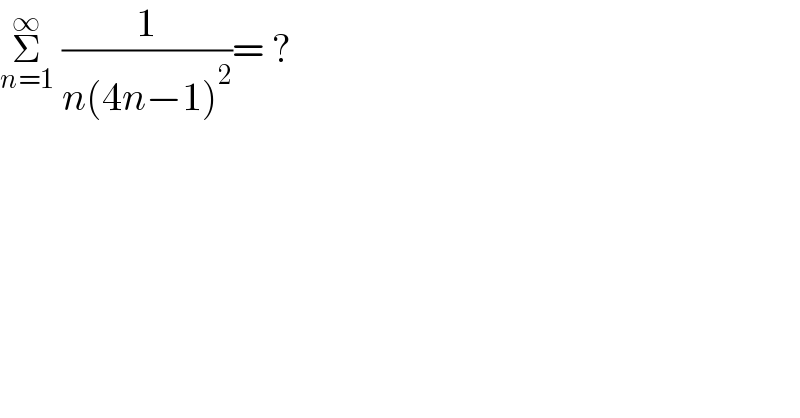
Σ_(n=1) ^∞ (1/(n(4n−1)^2 ))= ?

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}\left(\mathrm{4}{n}−\mathrm{1}\right)^{\mathrm{2}} }=\:? \\ $$

Answered by MrGaster last updated on 24/Dec/24

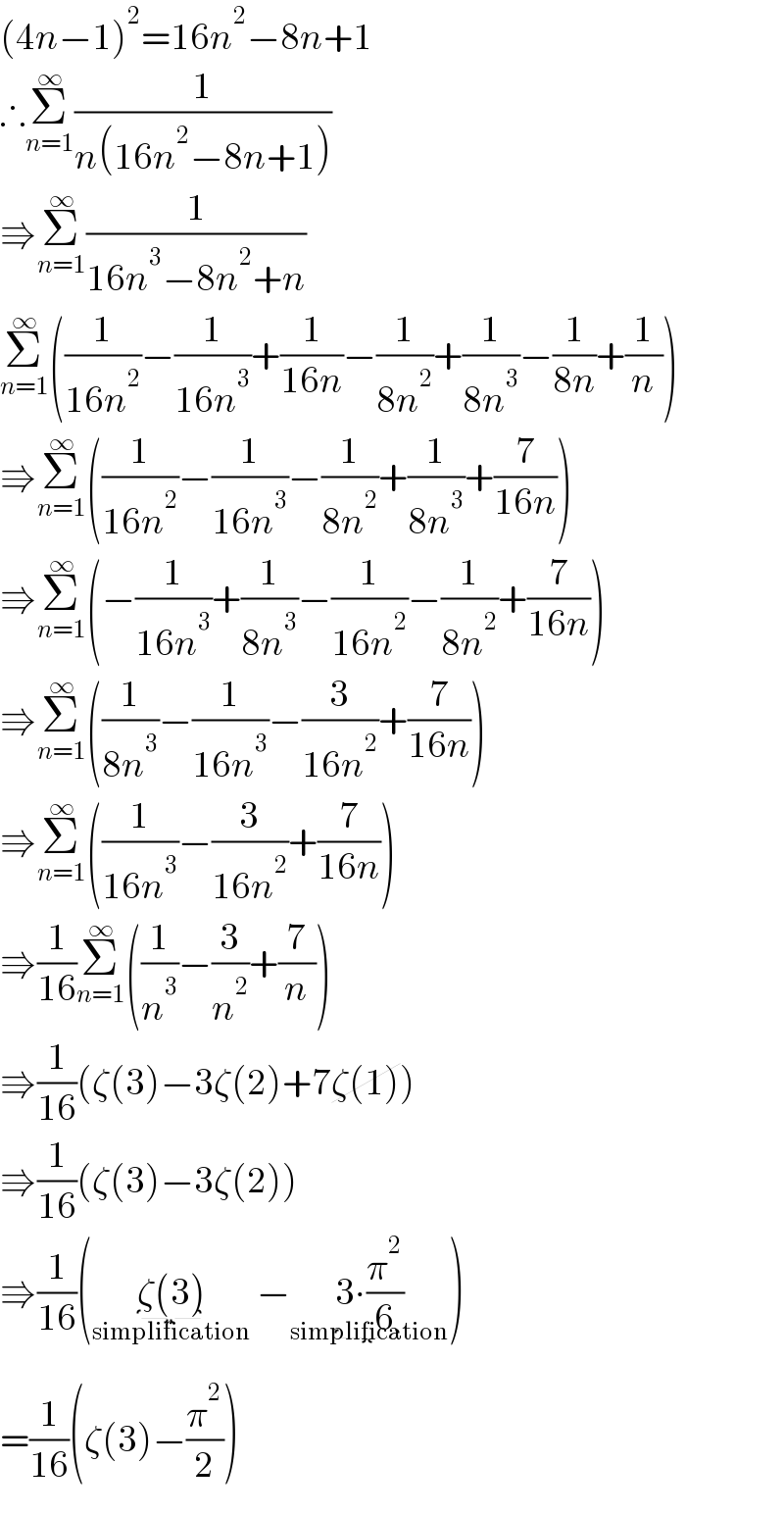
(4n−1)^2 =16n^2 −8n+1 ∴Σ_(n=1) ^∞ (1/(n(16n^2 −8n+1))) ⇛Σ_(n=1) ^∞ (1/(16n^3 −8n^2 +n)) Σ_(n=1) ^∞ ((1/(16n^2 ))−(1/(16n^3 ))+(1/(16n))−(1/(8n^2 ))+(1/(8n^3 ))−(1/(8n))+(1/n)) ⇛Σ_(n=1) ^∞ ((1/(16n^2 ))−(1/(16n^3 ))−(1/(8n^2 ))+(1/(8n^3 ))+(7/(16n))) ⇛Σ_(n=1) ^∞ (−(1/(16n^3 ))+(1/(8n^3 ))−(1/(16n^2 ))−(1/(8n^2 ))+(7/(16n))) ⇛Σ_(n=1) ^∞ ((1/(8n^3 ))−(1/(16n^3 ))−(3/(16n^2 ))+(7/(16n))) ⇛Σ_(n=1) ^∞ ((1/(16n^3 ))−(3/(16n^2 ))+(7/(16n))) ⇛(1/(16))Σ_(n=1) ^∞ ((1/n^3 )−(3/n^2 )+(7/n)) ⇛(1/(16))(ζ(3)−3ζ(2)+7ζ(1)) ⇛(1/(16))(ζ(3)−3ζ(2)) ⇛(1/(16))(ζ(3)_(simplification) −3∙(π^2 /6)_(simplification) ) =(1/(16))(ζ(3)−(π^2 /2))

$$\left(\mathrm{4}{n}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{16}{n}^{\mathrm{2}} −\mathrm{8}{n}+\mathrm{1} \\ $$$$\therefore\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left(\mathrm{16}{n}^{\mathrm{2}} −\mathrm{8}{n}+\mathrm{1}\right)} \\ $$$$\Rrightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{3}} −\mathrm{8}{n}^{\mathrm{2}} +{n}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{16}{n}}−\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{8}{n}}+\frac{\mathrm{1}}{{n}}\right) \\ $$$$\Rrightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{3}} }+\frac{\mathrm{7}}{\mathrm{16}{n}}\right) \\ $$$$\Rrightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{2}} }+\frac{\mathrm{7}}{\mathrm{16}{n}}\right) \\ $$$$\Rrightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{3}} }−\frac{\mathrm{3}}{\mathrm{16}{n}^{\mathrm{2}} }+\frac{\mathrm{7}}{\mathrm{16}{n}}\right) \\ $$$$\Rrightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{3}} }−\frac{\mathrm{3}}{\mathrm{16}{n}^{\mathrm{2}} }+\frac{\mathrm{7}}{\mathrm{16}{n}}\right) \\ $$$$\Rrightarrow\frac{\mathrm{1}}{\mathrm{16}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\frac{\mathrm{3}}{{n}^{\mathrm{2}} }+\frac{\mathrm{7}}{{n}}\right) \\ $$$$\Rrightarrow\frac{\mathrm{1}}{\mathrm{16}}\left(\zeta\left(\mathrm{3}\right)−\mathrm{3}\zeta\left(\mathrm{2}\right)+\mathrm{7}\cancel{\zeta\left(\mathrm{1}\right)}\right) \\ $$$$\Rrightarrow\frac{\mathrm{1}}{\mathrm{16}}\left(\zeta\left(\mathrm{3}\right)−\mathrm{3}\zeta\left(\mathrm{2}\right)\right) \\ $$$$\Rrightarrow\frac{\mathrm{1}}{\mathrm{16}}\left(\underset{\mathrm{simplification}} {\underbrace{\zeta\left(\mathrm{3}\right)}}\:−\underset{\mathrm{simplification}} {\underbrace{\mathrm{3}\centerdot\frac{\pi^{\mathrm{2}} }{\mathrm{6}}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left(\zeta\left(\mathrm{3}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com