Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 160289 by amin96 last updated on 27/Nov/21

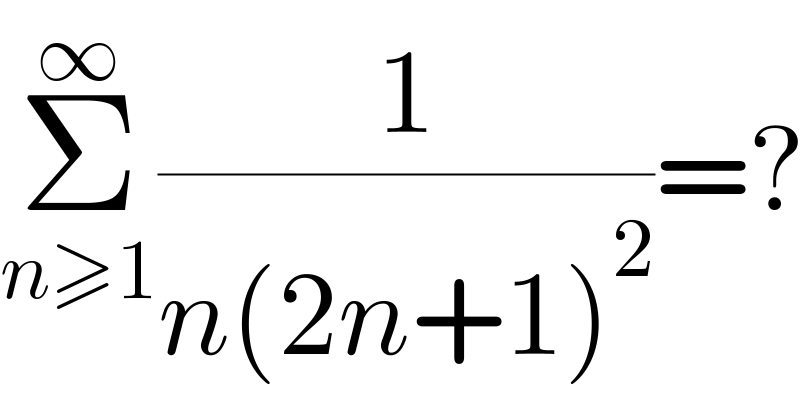
Σ_(n≥1) ^∞ (1/(n(2n+1)^2 ))=?

$$\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }=? \\ $$

Answered by qaz last updated on 27/Nov/21

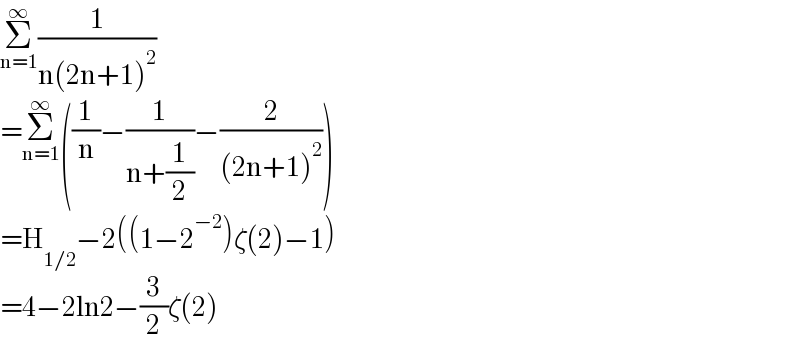
Σ_(n=1) ^∞ (1/(n(2n+1)^2 )) =Σ_(n=1) ^∞ ((1/n)−(1/(n+(1/2)))−(2/((2n+1)^2 ))) =H_(1/2) −2((1−2^(−2) )ζ(2)−1) =4−2ln2−(3/2)ζ(2)

$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}}−\frac{\mathrm{2}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=\mathrm{H}_{\mathrm{1}/\mathrm{2}} −\mathrm{2}\left(\left(\mathrm{1}−\mathrm{2}^{−\mathrm{2}} \right)\zeta\left(\mathrm{2}\right)−\mathrm{1}\right) \\ $$$$=\mathrm{4}−\mathrm{2ln2}−\frac{\mathrm{3}}{\mathrm{2}}\zeta\left(\mathrm{2}\right) \\ $$

Answered by mathmax by abdo last updated on 28/Nov/21

we decompose f(x)=(1/(x(2x+1)^2 )) ⇒f(x)=(a/x)+(b/(2x+1))+(c/((2x+1)^2 )) a=xf(x)∣_(x=0) =1 c=(2x+1)^2 f(x)∣_(x=−(1/2)) =−2 lim_(x→+∞) xf(x)=0=a+(b/2) ⇒(b/2)=−a ⇒b=−2 ⇒ f(x)=(1/x)−(2/(2x+1))−(2/((2x+1)^2 )) S_n =Σ_(k=1) ^n (1/(k(2k+1)^2 )) ⇒S_n =Σ_(k=1) ^n f(k)=Σ_(k=1) ^n ((1/k)−(2/(2k+1))−(2/((2k+1)^2 ))) =Σ_(k=1) ^n (1/k)−2Σ_(k=1) ^n (1/(2k+1))−2Σ_(k=1) ^n (1/((2k+1)^2 )) Σ_(k=1) ^n (1/k)=H_n Σ_(k=1) ^n (1/(2k+1))=(1/3)+(1/5)+...+(1/(2n+1))=1+(1/2)+(1/3)+(1/4)+....+(1/(2n))+(1/(2n+1)) −1−(1/2)−(1/4)−...−(1/(2n))=H_(2n+1) −1−(1/2)H_n Σ_(k=1) ^n (1/((2k+1)^2 ))→Σ_(k=1) ^∞ (1/((2k+1)^2 ))=(π^2 /8)−1 due to Σ (1/k^2 )=(1/4)Σ(1/k^2 )+Σ_(k=0) ^∞ (1/((2k+1)^2 )) ⇒Σ_(k=0) ^∞ (1/((2k+1)^2 ))=(3/4)(π^2 /6)=(π^2 /8) Σ_(k=1) ^n (1/k)−2Σ_(k=1) ^n (1/(2k+1))=H_n −2{H_(2n+1) −1−(1/2)H_n } =2H_n −2H_(2n+1) +2∼2(ln(n)+γ)−2(ln(2n+1)+γ)+2 =2ln((n/(2n+1)))+2→2ln((1/2))+2=2−2ln2 ⇒ lim_(n→+∞) S_n =2−2ln2−2{(π^2 /8)−1} =2−2ln2−(π^2 /4) +2=4−2ln2−(π^2 /4)

$$\mathrm{we}\:\mathrm{decompose}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{a}}{\mathrm{x}}+\frac{\mathrm{b}}{\mathrm{2x}+\mathrm{1}}+\frac{\mathrm{c}}{\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{a}=\mathrm{xf}\left(\mathrm{x}\right)\mid_{\mathrm{x}=\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{c}=\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{f}\left(\mathrm{x}\right)\mid_{\mathrm{x}=−\frac{\mathrm{1}}{\mathrm{2}}} \:\:=−\mathrm{2} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xf}\left(\mathrm{x}\right)=\mathrm{0}=\mathrm{a}+\frac{\mathrm{b}}{\mathrm{2}}\:\Rightarrow\frac{\mathrm{b}}{\mathrm{2}}=−\mathrm{a}\:\Rightarrow\mathrm{b}=−\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{2}}{\mathrm{2x}+\mathrm{1}}−\frac{\mathrm{2}}{\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \mathrm{f}\left(\mathrm{k}\right)=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{2}}{\mathrm{2k}+\mathrm{1}}−\frac{\mathrm{2}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}−\mathrm{2}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{2k}+\mathrm{1}}−\mathrm{2}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}=\mathrm{H}_{\mathrm{n}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{2k}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+...+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+....+\frac{\mathrm{1}}{\mathrm{2n}}+\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}} \\ $$$$−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}−...−\frac{\mathrm{1}}{\mathrm{2n}}=\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }\rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\mathrm{1}\:\mathrm{due}\:\mathrm{to} \\ $$$$\Sigma\:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\Sigma\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }+\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}}\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}−\mathrm{2}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{2k}+\mathrm{1}}=\mathrm{H}_{\mathrm{n}} −\mathrm{2}\left\{\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} \right\} \\ $$$$=\mathrm{2H}_{\mathrm{n}} −\mathrm{2H}_{\mathrm{2n}+\mathrm{1}} \:+\mathrm{2}\sim\mathrm{2}\left(\mathrm{ln}\left(\mathrm{n}\right)+\gamma\right)−\mathrm{2}\left(\mathrm{ln}\left(\mathrm{2n}+\mathrm{1}\right)+\gamma\right)+\mathrm{2} \\ $$$$=\mathrm{2ln}\left(\frac{\mathrm{n}}{\mathrm{2n}+\mathrm{1}}\right)+\mathrm{2}\rightarrow\mathrm{2ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}=\mathrm{2}−\mathrm{2ln2}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{S}_{\mathrm{n}} =\mathrm{2}−\mathrm{2ln2}−\mathrm{2}\left\{\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\mathrm{1}\right\} \\ $$$$=\mathrm{2}−\mathrm{2ln2}−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:+\mathrm{2}=\mathrm{4}−\mathrm{2ln2}−\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com