
Question Number 147737 by liberty last updated on 23/Jul/21
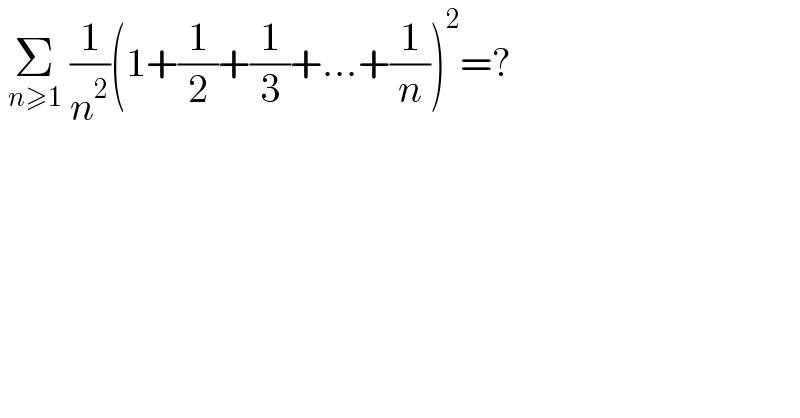
$$\:\underset{{n}\geqslant\mathrm{1}} {\sum}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+...+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} =? \\ $$
Answered by ArielVyny last updated on 24/Jul/21
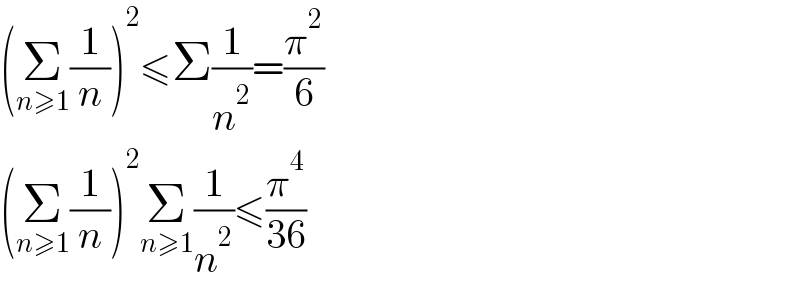
$$\left(\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} \leqslant\Sigma\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\left(\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} \underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\leqslant\frac{\pi^{\mathrm{4}} }{\mathrm{36}} \\ $$
