Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 145025 by mathdanisur last updated on 01/Jul/21

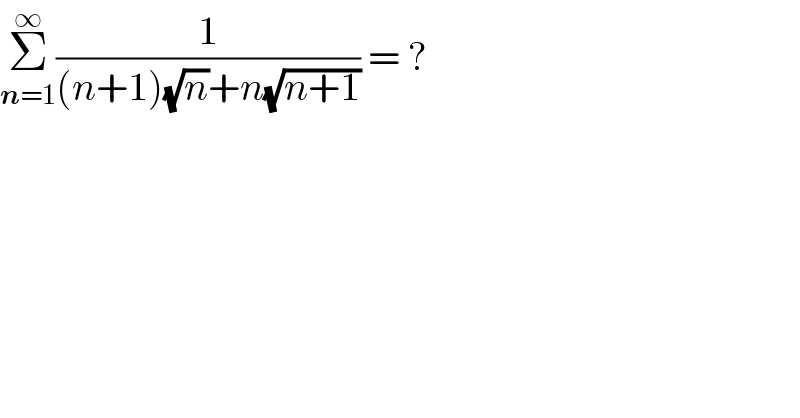
Σ_(n=1) ^∞ (1/((n+1)(√n)+n(√(n+1)))) = ?

$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\sqrt{{n}}+{n}\sqrt{{n}+\mathrm{1}}}\:=\:? \\ $$

Answered by phally last updated on 01/Jul/21

=Σ_(n=1) ^∞ (((n+1)(√n)−n(√(n+1)))/([(n+1)(√n)]^2 −(n(√(n+1)))^2 )) =Σ_(n=1) ^∞ (((n+1)(√n)−n(√(n+1)))/( (√n^2 )(n^2 +2n+1)−n^2 (n+1))) =Σ_(n=1) ^∞ (((n+1)(√n)−n(√(n+1)))/(n^3 +2n^2 +n−n^3 −n^2 )) =Σ_(n=1) ^∞ (((n+1)(√n)−n(√(n+1)))/(n(n+1))) =Σ_(n=1) ^∞ ((1/( (√n)))−(1/( (√(n+1))))) =1−(1/( (√(n+1))))

$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{n}}−\mathrm{n}\sqrt{\mathrm{n}+\mathrm{1}}}{\left[\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{n}}\right]^{\mathrm{2}} −\left(\mathrm{n}\sqrt{\mathrm{n}+\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{n}}−\mathrm{n}\sqrt{\mathrm{n}+\mathrm{1}}}{\:\sqrt{\mathrm{n}^{\mathrm{2}} }\left(\mathrm{n}^{\mathrm{2}} +\mathrm{2n}+\mathrm{1}\right)−\mathrm{n}^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{n}}−\mathrm{n}\sqrt{\mathrm{n}+\mathrm{1}}}{\mathrm{n}^{\mathrm{3}} +\mathrm{2n}^{\mathrm{2}} +\mathrm{n}−\mathrm{n}^{\mathrm{3}} −\mathrm{n}^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{n}+\mathrm{1}\right)\sqrt{\mathrm{n}}−\mathrm{n}\sqrt{\mathrm{n}+\mathrm{1}}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}+\mathrm{1}}}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}+\mathrm{1}}} \\ $$

Commented by mathdanisur last updated on 01/Jul/21

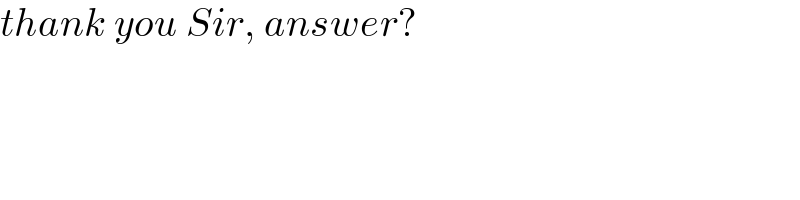
thank you Sir, answer?

$${thank}\:{you}\:{Sir},\:{answer}? \\ $$

Commented by JDamian last updated on 01/Jul/21

you only have to get now the limit when n --> inf

Answered by mathmax by abdo last updated on 01/Jul/21

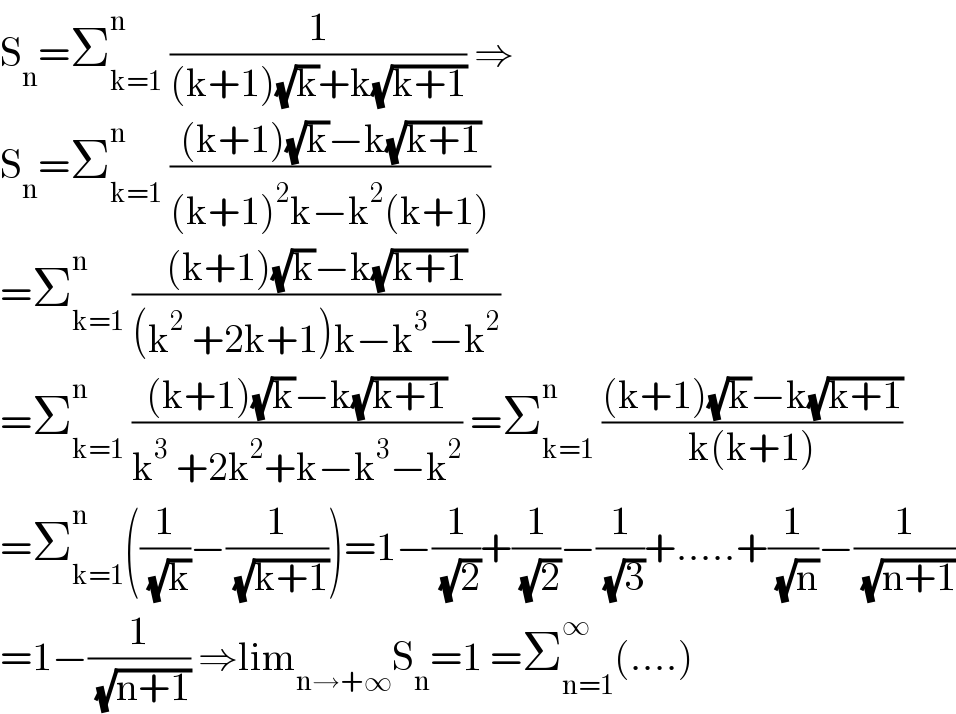
S_n =Σ_(k=1) ^n (1/((k+1)(√k)+k(√(k+1)))) ⇒ S_n =Σ_(k=1) ^n (((k+1)(√k)−k(√(k+1)))/((k+1)^2 k−k^2 (k+1))) =Σ_(k=1) ^n (((k+1)(√k)−k(√(k+1)))/((k^2 +2k+1)k−k^3 −k^2 )) =Σ_(k=1) ^n (((k+1)(√k)−k(√(k+1)))/(k^3 +2k^2 +k−k^3 −k^2 )) =Σ_(k=1) ^n (((k+1)(√k)−k(√(k+1)))/(k(k+1))) =Σ_(k=1) ^n ((1/( (√k)))−(1/( (√(k+1)))))=1−(1/( (√2)))+(1/( (√2)))−(1/( (√3)))+.....+(1/( (√n)))−(1/( (√(n+1)))) =1−(1/( (√(n+1)))) ⇒lim_(n→+∞) S_n =1 =Σ_(n=1) ^∞ (....)

$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)\sqrt{\mathrm{k}}+\mathrm{k}\sqrt{\mathrm{k}+\mathrm{1}}}\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(\mathrm{k}+\mathrm{1}\right)\sqrt{\mathrm{k}}−\mathrm{k}\sqrt{\mathrm{k}+\mathrm{1}}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{k}−\mathrm{k}^{\mathrm{2}} \left(\mathrm{k}+\mathrm{1}\right)} \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(\mathrm{k}+\mathrm{1}\right)\sqrt{\mathrm{k}}−\mathrm{k}\sqrt{\mathrm{k}+\mathrm{1}}}{\left(\mathrm{k}^{\mathrm{2}} \:+\mathrm{2k}+\mathrm{1}\right)\mathrm{k}−\mathrm{k}^{\mathrm{3}} −\mathrm{k}^{\mathrm{2}} } \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(\mathrm{k}+\mathrm{1}\right)\sqrt{\mathrm{k}}−\mathrm{k}\sqrt{\mathrm{k}+\mathrm{1}}}{\mathrm{k}^{\mathrm{3}} \:+\mathrm{2k}^{\mathrm{2}} +\mathrm{k}−\mathrm{k}^{\mathrm{3}} −\mathrm{k}^{\mathrm{2}} }\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\left(\mathrm{k}+\mathrm{1}\right)\sqrt{\mathrm{k}}−\mathrm{k}\sqrt{\mathrm{k}+\mathrm{1}}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)} \\ $$$$=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{k}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{k}+\mathrm{1}}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+.....+\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}+\mathrm{1}}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}+\mathrm{1}}}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{S}_{\mathrm{n}} =\mathrm{1}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(....\right) \\ $$

Commented by mathdanisur last updated on 01/Jul/21

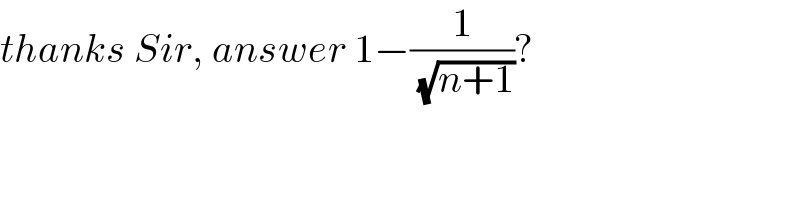
thanks Sir, answer 1−(1/( (√(n+1))))?

$${thanks}\:{Sir},\:{answer}\:\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}}? \\ $$

Commented by mathmax by abdo last updated on 01/Jul/21

no answer is 1

$$\mathrm{no}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{1} \\ $$

Commented by mathdanisur last updated on 01/Jul/21

thanks Sir

$${thanks}\:{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com