Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 161622 by amin96 last updated on 20/Dec/21

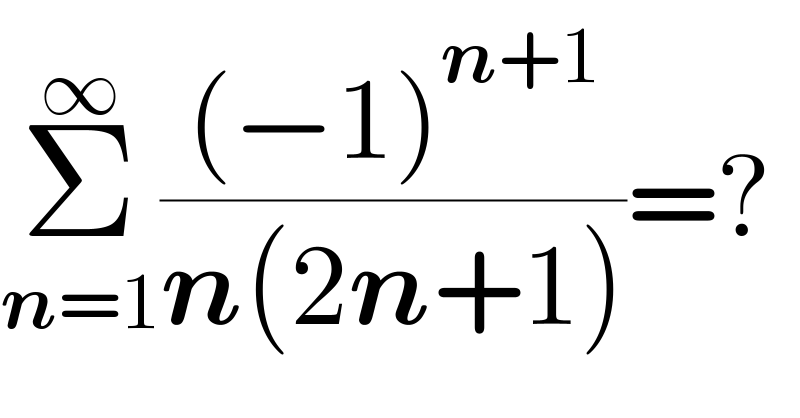
Σ_(n=1) ^∞ (((−1)^(n+1) )/(n(2n+1)))=?

$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}+\mathrm{1}} }{\boldsymbol{{n}}\left(\mathrm{2}\boldsymbol{{n}}+\mathrm{1}\right)}=? \\ $$

Answered by mathmax by abdo last updated on 20/Dec/21

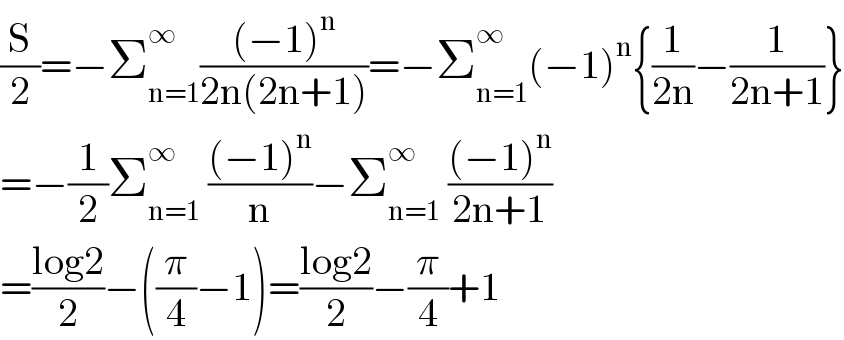
(S/2)=−Σ_(n=1) ^∞ (((−1)^n )/(2n(2n+1)))=−Σ_(n=1) ^∞ (−1)^n {(1/(2n))−(1/(2n+1))} =−(1/2)Σ_(n=1) ^∞ (((−1)^n )/n)−Σ_(n=1) ^∞ (((−1)^n )/(2n+1)) =((log2)/2)−((π/4)−1)=((log2)/2)−(π/4)+1

$$\frac{\mathrm{S}}{\mathrm{2}}=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}\left(\mathrm{2n}+\mathrm{1}\right)}=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \left\{\frac{\mathrm{1}}{\mathrm{2n}}−\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{log2}}{\mathrm{2}}−\left(\frac{\pi}{\mathrm{4}}−\mathrm{1}\right)=\frac{\mathrm{log2}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}+\mathrm{1} \\ $$

Commented by mathmax by abdo last updated on 20/Dec/21

⇒S=log2−(π/2) +2

$$\Rightarrow\mathrm{S}=\mathrm{log2}−\frac{\pi}{\mathrm{2}}\:+\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com