
Question Number 130886 by Khalmohmmad last updated on 30/Jan/21

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}+\mathrm{2}^{{n}} }{\mathrm{3}^{{n}} } \\ $$
Answered by EDWIN88 last updated on 30/Jan/21
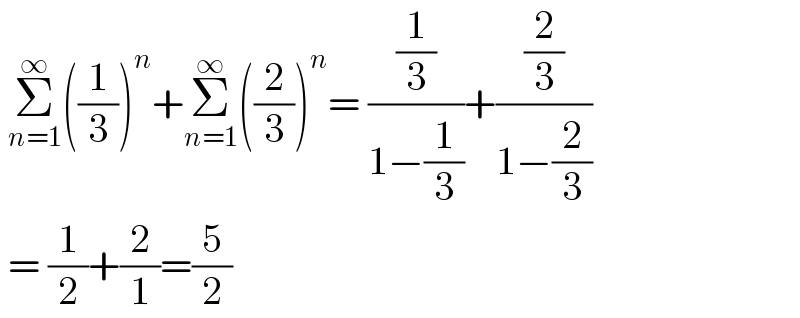
$$\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{{n}} +\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} =\:\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}+\frac{\frac{\mathrm{2}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{1}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$
