
Question Number 195904 by York12 last updated on 13/Aug/23
![Σ_(n=0) ^∞ [((2^n (2n)!)/(3^(2n+1) (n+1)!n!))]=λ Evaluate (λ)](Q195904.png)
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{2}^{{n}} \left(\mathrm{2}{n}\right)!}{\mathrm{3}^{\mathrm{2}{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)!{n}!}\right]=\lambda \\ $$$${Evaluate}\:\left(\lambda\right) \\ $$
Answered by qaz last updated on 13/Aug/23
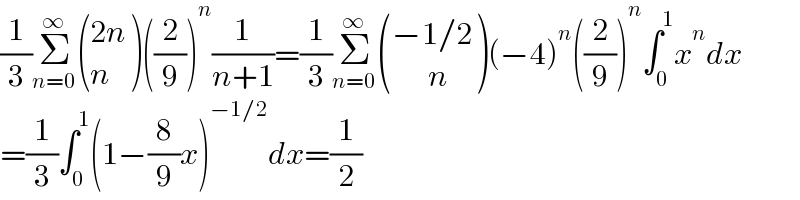
$$\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{{n}}\end{pmatrix}\left(\frac{\mathrm{2}}{\mathrm{9}}\right)^{{n}} \frac{\mathrm{1}}{{n}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{−\mathrm{1}/\mathrm{2}}\\{\:\:\:\:\:\:{n}}\end{pmatrix}\left(−\mathrm{4}\right)^{{n}} \left(\frac{\mathrm{2}}{\mathrm{9}}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{8}}{\mathrm{9}}{x}\right)^{−\mathrm{1}/\mathrm{2}} {dx}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by York12 last updated on 13/Aug/23

$${thanks} \\ $$
