Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 138598 by qaz last updated on 15/Apr/21

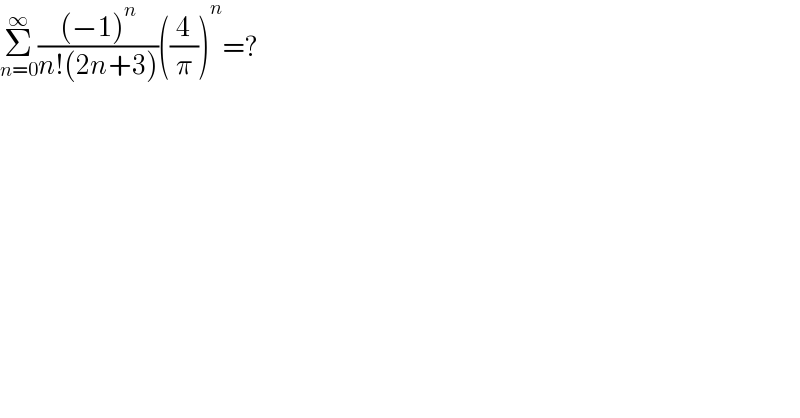
Σ_(n=0) ^∞ (((−1)^n )/(n!(2n+3)))((4/π))^n =?

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!\left(\mathrm{2}{n}+\mathrm{3}\right)}\left(\frac{\mathrm{4}}{\pi}\right)^{{n}} =? \\ $$

Answered by mr W last updated on 15/Apr/21

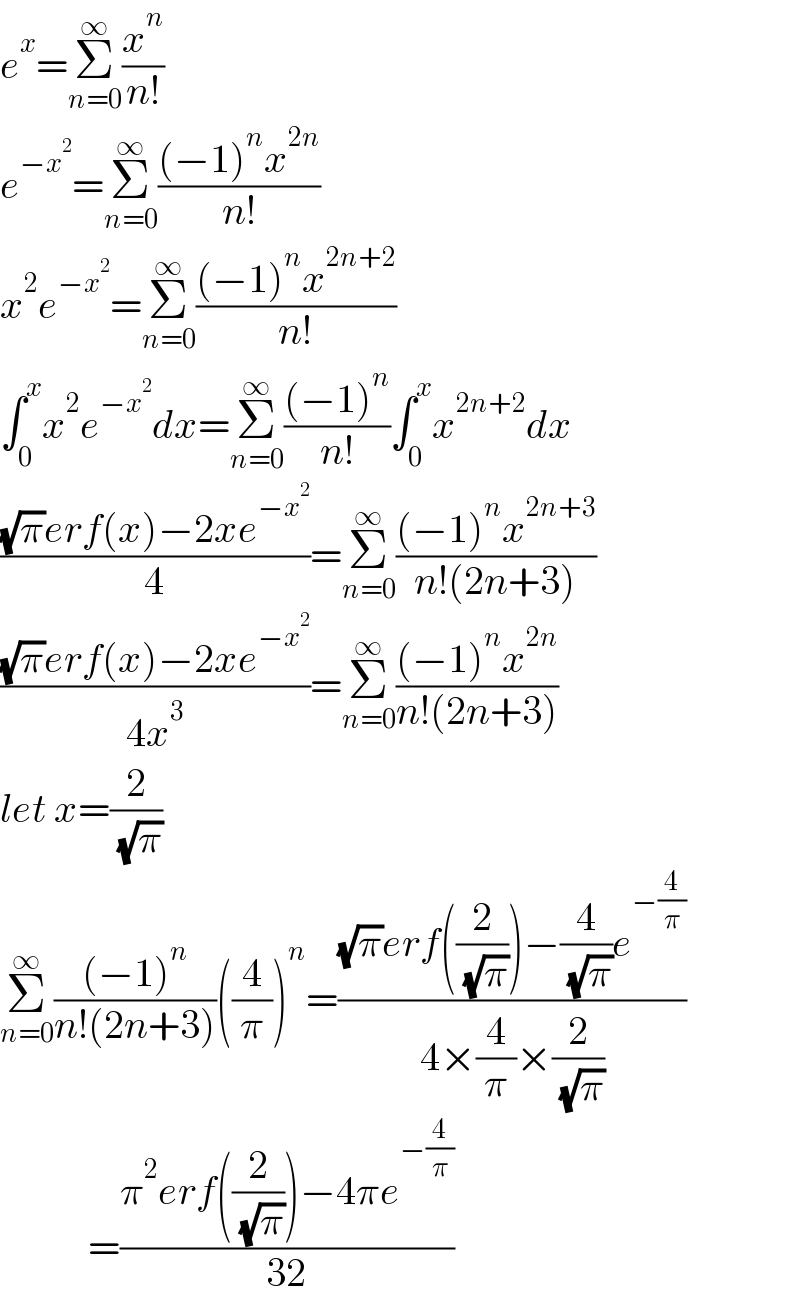
e^x =Σ_(n=0) ^∞ (x^n /(n!)) e^(−x^2 ) =Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!)) x^2 e^(−x^2 ) =Σ_(n=0) ^∞ (((−1)^n x^(2n+2) )/(n!)) ∫_0 ^x x^2 e^(−x^2 ) dx=Σ_(n=0) ^∞ (((−1)^n )/(n!))∫_0 ^x x^(2n+2) dx (((√π)erf(x)−2xe^(−x^2 ) )/4)=Σ_(n=0) ^∞ (((−1)^n x^(2n+3) )/(n!(2n+3))) (((√π)erf(x)−2xe^(−x^2 ) )/(4x^3 ))=Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(n!(2n+3))) let x=(2/( (√π))) Σ_(n=0) ^∞ (((−1)^n )/(n!(2n+3)))((4/π))^n =(((√π)erf((2/( (√π))))−(4/( (√π)))e^(−(4/π)) )/(4×(4/π)×(2/( (√π))))) =((π^2 erf((2/( (√π))))−4πe^(−(4/π)) )/(32))

$${e}^{{x}} =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$${e}^{−{x}^{\mathrm{2}} } =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{{n}!} \\ $$$${x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } =\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{2}} }{{n}!} \\ $$$$\int_{\mathrm{0}} ^{{x}} {x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\int_{\mathrm{0}} ^{{x}} {x}^{\mathrm{2}{n}+\mathrm{2}} {dx} \\ $$$$\frac{\sqrt{\pi}{erf}\left({x}\right)−\mathrm{2}{xe}^{−{x}^{\mathrm{2}} } }{\mathrm{4}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{3}} }{{n}!\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$$\frac{\sqrt{\pi}{erf}\left({x}\right)−\mathrm{2}{xe}^{−{x}^{\mathrm{2}} } }{\mathrm{4}{x}^{\mathrm{3}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{{n}!\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$${let}\:{x}=\frac{\mathrm{2}}{\:\sqrt{\pi}} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!\left(\mathrm{2}{n}+\mathrm{3}\right)}\left(\frac{\mathrm{4}}{\pi}\right)^{{n}} =\frac{\sqrt{\pi}{erf}\left(\frac{\mathrm{2}}{\:\sqrt{\pi}}\right)−\frac{\mathrm{4}}{\:\sqrt{\pi}}{e}^{−\frac{\mathrm{4}}{\pi}} }{\mathrm{4}×\frac{\mathrm{4}}{\pi}×\frac{\mathrm{2}}{\:\sqrt{\pi}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\pi^{\mathrm{2}} {erf}\left(\frac{\mathrm{2}}{\:\sqrt{\pi}}\right)−\mathrm{4}\pi{e}^{−\frac{\mathrm{4}}{\pi}} }{\mathrm{32}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com