Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 155133 by amin96 last updated on 25/Sep/21

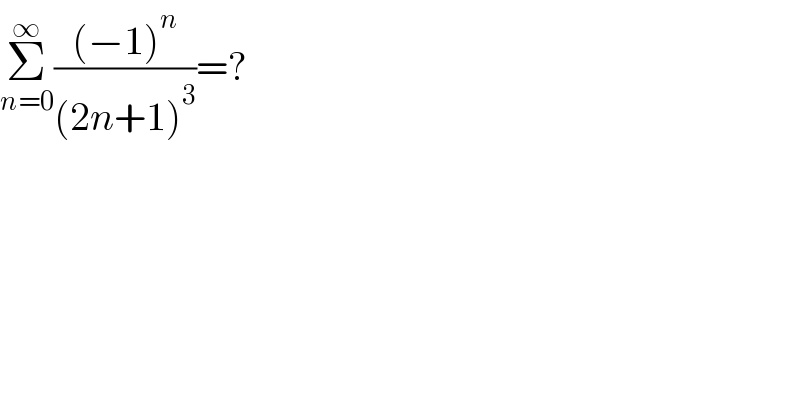
Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 ))=?

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }=? \\ $$

Answered by mnjuly1970 last updated on 26/Sep/21

(π^( 3) /(32))

$$\:\:\:\frac{\pi^{\:\mathrm{3}} }{\mathrm{32}} \\ $$

Answered by qaz last updated on 26/Sep/21

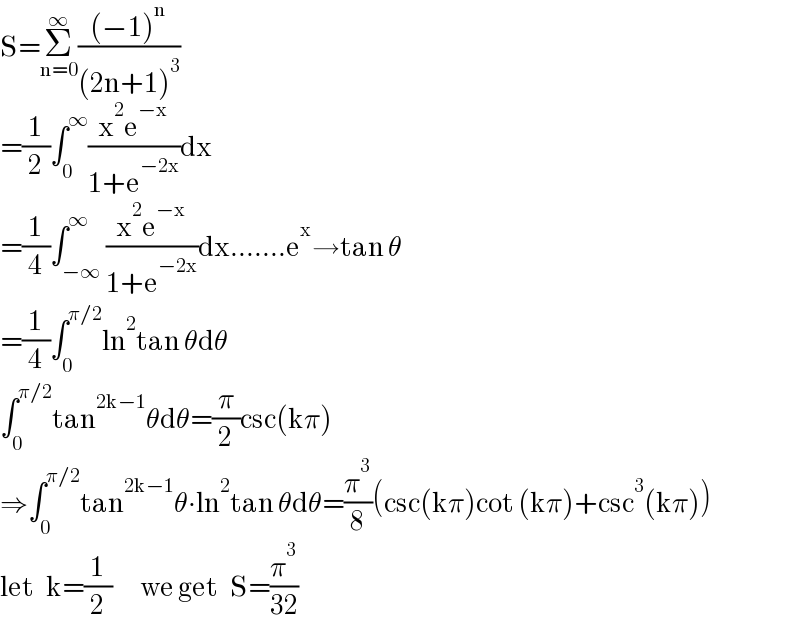
S=Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^3 )) =(1/2)∫_0 ^∞ ((x^2 e^(−x) )/(1+e^(−2x) ))dx =(1/4)∫_(−∞) ^∞ ((x^2 e^(−x) )/(1+e^(−2x) ))dx.......e^x →tan θ =(1/4)∫_0 ^(π/2) ln^2 tan θdθ ∫_0 ^(π/2) tan^(2k−1) θdθ=(π/2)csc(kπ) ⇒∫_0 ^(π/2) tan^(2k−1) θ∙ln^2 tan θdθ=(π^3 /8)(csc(kπ)cot (kπ)+csc^3 (kπ)) let k=(1/2) we get S=(π^3 /(32))

$$\mathrm{S}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{2x}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{−\infty} ^{\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{2x}} }\mathrm{dx}.......\mathrm{e}^{\mathrm{x}} \rightarrow\mathrm{tan}\:\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{ln}^{\mathrm{2}} \mathrm{tan}\:\theta\mathrm{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{tan}^{\mathrm{2k}−\mathrm{1}} \theta\mathrm{d}\theta=\frac{\pi}{\mathrm{2}}\mathrm{csc}\left(\mathrm{k}\pi\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{tan}^{\mathrm{2k}−\mathrm{1}} \theta\centerdot\mathrm{ln}^{\mathrm{2}} \mathrm{tan}\:\theta\mathrm{d}\theta=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}\left(\mathrm{csc}\left(\mathrm{k}\pi\right)\mathrm{cot}\:\left(\mathrm{k}\pi\right)+\mathrm{csc}^{\mathrm{3}} \left(\mathrm{k}\pi\right)\right) \\ $$$$\mathrm{let}\:\:\:\mathrm{k}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\mathrm{we}\:\mathrm{get}\:\:\:\mathrm{S}=\frac{\pi^{\mathrm{3}} }{\mathrm{32}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com