
Question Number 153009 by SANOGO last updated on 04/Sep/21
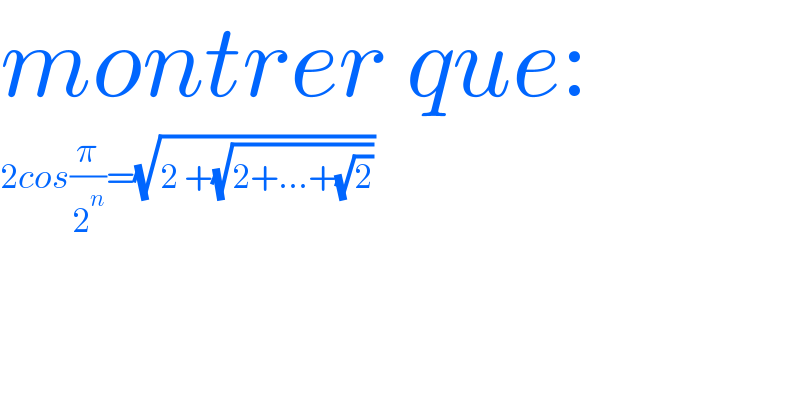
$${montrer}\:{que}: \\ $$$$\mathrm{2}{cos}\frac{\pi}{\mathrm{2}^{{n}} }=\sqrt{\mathrm{2}\:+\sqrt{\mathrm{2}+...+\sqrt{\mathrm{2}}}} \\ $$$$ \\ $$
Commented by mr W last updated on 04/Sep/21

$${please}\:{make}\:{your}\:{posts}\:{better}\:{readable}! \\ $$$${try}\:{to}\:{set}\:{the}\:{defaut}\:{font}\:{size}\:\mathrm{20}. \\ $$$${try}\:{to}\:{avoid}\:{using}\:{extremly}\:{large}\:{or} \\ $$$${extremly}\:{small}\:{fonts}! \\ $$
Commented by SANOGO last updated on 04/Sep/21

$${ok}\:{thank}\:{you}\:{i}\:{understood} \\ $$
Answered by puissant last updated on 04/Sep/21
![montrons alors que ∀n∈N, 2cos(π/2^n )=(√(2+(√(2+....+(√2))))) ⇒ cos(π/2^n )=(1/2)(√(2+(√(2+(√(2+..(√2))))))) →pour n=1 la propriete^� est vraie.. →soit n∈N, supposons la propriete^� vraie au rang n et prouvons au rang n+1. Remarquons au pre^� alable que ∀x∈[0;(π/2)] comme cos^2 x=((cos2x+1)/2)⇒cos((x/2))=(√((cosx+1)/2)) et cos((π/2^(n+1) ))=cos((1/2)((π/2^n ))) =(√((1/2)(cos((π/2^n ))+1))) =(√((1/2)((1/2)(√(2+(√(2+...+(√2)))))+1))) on a ainsi n radicaux d′apres l′hypothese de reccurence. =(1/2)(√(2+(√(2+...+(√2))))) (n+1 radicaux) on prouve ainsi la propriete^� par reccurence..](Q153014.png)
$${montrons}\:{alors}\:{que}\:\forall{n}\in\mathbb{N},\:\mathrm{2}{cos}\frac{\pi}{\mathrm{2}^{{n}} }=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+....+\sqrt{\mathrm{2}}}} \\ $$$$\Rightarrow\:{cos}\frac{\pi}{\mathrm{2}^{{n}} }=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+..\sqrt{\mathrm{2}}}}} \\ $$$$\rightarrow{pour}\:{n}=\mathrm{1}\:{la}\:{propriet}\acute {{e}}\:{est}\:{vraie}.. \\ $$$$\rightarrow{soit}\:{n}\in\mathbb{N},\:{supposons}\:{la}\:{propriet}\acute {{e}}\:{vraie} \\ $$$${au}\:{rang}\:{n}\:{et}\:{prouvons}\:{au}\:{rang}\:{n}+\mathrm{1}. \\ $$$${Remarquons}\:{au}\:{pr}\acute {{e}alable}\:{que}\:\forall{x}\in\left[\mathrm{0};\frac{\pi}{\mathrm{2}}\right] \\ $$$${comme}\:{cos}^{\mathrm{2}} {x}=\frac{{cos}\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}}\Rightarrow{cos}\left(\frac{{x}}{\mathrm{2}}\right)=\sqrt{\frac{{cosx}+\mathrm{1}}{\mathrm{2}}} \\ $$$${et}\:{cos}\left(\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right)={cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)\right) \\ $$$$=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)+\mathrm{1}\right)} \\ $$$$=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+...+\sqrt{\mathrm{2}}}}+\mathrm{1}\right)}\:{on}\:{a}\:{ainsi} \\ $$$${n}\:{radicaux}\:{d}'{apres}\:{l}'{hypothese}\:{de}\:{reccurence}. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+...+\sqrt{\mathrm{2}}}}\:\:\left({n}+\mathrm{1}\:{radicaux}\right) \\ $$$${on}\:{prouve}\:{ainsi}\:{la}\:{propriet}\acute {{e}}\:{par}\:{reccurence}.. \\ $$
Commented by SANOGO last updated on 04/Sep/21

$${merci}\:{bien}\:{que}\:{Dieu}\:{te}\:{benisse} \\ $$
Answered by som(math1967) last updated on 04/Sep/21
![cos(𝛑/4)=(1/( (√2))) 2cos(𝛑/4)=(√2) ∴2cos(𝛑/2^2 )=(√2) cos(𝛑/8)=(√((1+cos(𝛑/4))/2)) [∵cos(𝛉/2)=(√((1+cos𝛉)/2)) ] cos(𝛑/8)=(√(((√2)+1)/(2(√2))))=(√((2+(√2))/4))= 2cos(𝛑/2^3 )=(√(2+(√2))) same way 2cos(𝛑/2^4 )=(√(2+(√(2+(√2))))) 2cos(𝛑/2^5 )=(√(2+(√(2+(√(2+(√2))))))) .......2cos(𝛑/2^n )=(√(2+(√(2+(√(2+...(√2)))))))](Q153015.png)
$$\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{4}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{2}\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{4}}=\sqrt{\mathrm{2}}\:\therefore\mathrm{2}\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{2}^{\mathrm{2}} }=\sqrt{\mathrm{2}} \\ $$$$\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{8}}=\sqrt{\frac{\mathrm{1}+\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{4}}}{\mathrm{2}}}\:\:\left[\because\boldsymbol{{cos}}\frac{\boldsymbol{\theta}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}+\boldsymbol{{cos}\theta}}{\mathrm{2}}}\:\right] \\ $$$$\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{8}}=\sqrt{\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}}=\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{4}}}= \\ $$$$\mathrm{2}\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{2}^{\mathrm{3}} }=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}} \\ $$$${same}\:\boldsymbol{{way}}\:\:\mathrm{2}\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{2}^{\mathrm{4}} }=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}} \\ $$$$\mathrm{2}\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{2}^{\mathrm{5}} }=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}} \\ $$$$.......\mathrm{2}\boldsymbol{{cos}}\frac{\boldsymbol{\pi}}{\mathrm{2}^{\boldsymbol{{n}}} }=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+...\sqrt{\mathrm{2}}}}} \\ $$
Commented by SANOGO last updated on 04/Sep/21
$${merci}\:{beaucou}\:{le}\:{dur} \\ $$
Answered by Jonathanwaweh last updated on 05/Sep/21

$${montrer}\:{qu}: \\ $$$$\mathrm{2}{cos}\frac{\pi}{\mathrm{2}^{{n}} }=\sqrt{\mathrm{2}\:+\sqrt{\mathrm{2}+...+\sqrt{\mathrm{2}}}} \\ $$$${posons}\:{U}_{{n}} =\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+...+\sqrt{\mathrm{2}\:}}}\:{alors}\:{U}_{{n}+\mathrm{1}} =\sqrt{{U}_{{n}} +\mathrm{2}} \\ $$$${soit}\:{p}\left({n}\right)\::\forall{n}\epsilon{N}\:{n}\geqslant\mathrm{2}\:\mathrm{2}{cos}\frac{\Pi}{\mathrm{2}^{{n}} }={U}_{{n}} \\ $$$$\mathrm{1}−{initialisation}\left({facile}\right) \\ $$$$\mathrm{2}−{heredite} \\ $$$${pour}\:{n}\geqslant\mathrm{2}\:{fixe}^{'} \:{supposons}\:{p}\left({n}\right)\:{vraie}\:{et}\:{montrons}\:{que}\:{p}\left({n}+\mathrm{1}\right)\:{l}'{est}\:{aussi} \\ $$$${ie}\:\mathrm{2}{cos}\frac{\Pi}{\mathrm{2}^{{n}+\mathrm{1}} }={U}_{{n}+\mathrm{1}} .\:{on}\:{a}\:{cos}\left(\frac{\Pi}{\mathrm{2}^{{n}} }\right)={cos}\left(\frac{\Pi}{\mathrm{2}^{{n}+\mathrm{1}} }×\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\Pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right)−\mathrm{1} \\ $$$${donc}\:\mathrm{2}{cos}\left(\frac{\Pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right)=\mathrm{4}{cos}^{\mathrm{2}} \left(\frac{\Pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right)−\mathrm{2} \\ $$$${ie}\:\sqrt{\mathrm{2}{cos}\left(\frac{\Pi}{\mathrm{2}^{{n}} }\right)+\mathrm{2}}=\mathrm{2}{cos}\left(\frac{\Pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right) \\ $$$${d}^{'} {ou}\:{ona}\:{U}_{{n}+\mathrm{1}} =\mathrm{2}{cos}\left(\frac{\Pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right) \\ $$$${conclusion}:... \\ $$
Commented by SANOGO last updated on 05/Sep/21
$${merci}\:{bien}\:{mon}\:{chef} \\ $$
