Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 132474 by bemath last updated on 14/Feb/21

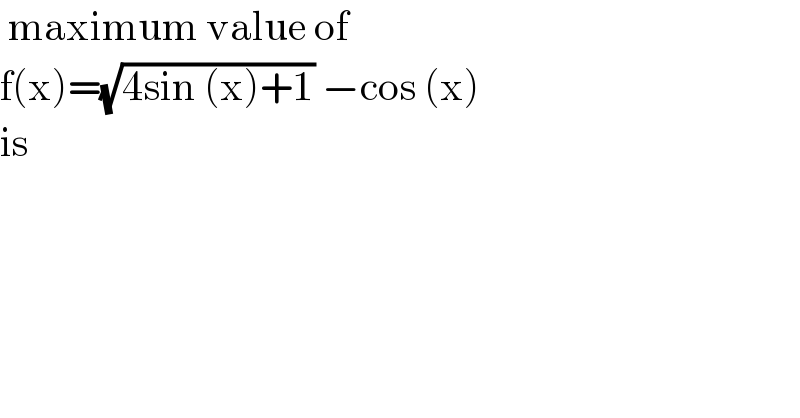
maximum value of f(x)=(√(4sin (x)+1)) −cos (x) is

$$\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{4sin}\:\left(\mathrm{x}\right)+\mathrm{1}}\:−\mathrm{cos}\:\left(\mathrm{x}\right) \\ $$$$\mathrm{is}\: \\ $$

Commented by EDWIN88 last updated on 14/Feb/21

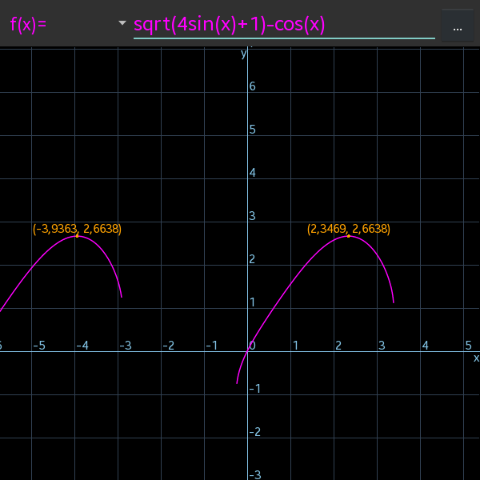
Commented by bemath last updated on 14/Feb/21

approximation

$$\mathrm{approximation} \\ $$

Answered by mr W last updated on 14/Feb/21

((df(x))/dx)=((2 cos x)/( (√(4 sin x+1))))+sin x=0 ((4 cos^2 x)/( 4 sin x+1))=sin^2 x ((4(1−sin^2 x))/( 4 sin x+1))=sin^2 x 4sin^3 x+5 sin^2 x−4=0 (1/(sin^3 x))−(5/(4 sin x))−1=0 Δ=(−(1/2))^2 +(−(5/(12)))^3 =((307)/(1728))>0 ⇒(1/(sin x))=(1/2)(((((√(921))/9)+4))^(1/3) −((((√(921))/9)−4))^(1/3) ) ⇒sin x=(2/( ((((√(921))/9)+4))^(1/3) −((((√(921))/9)−4))^(1/3) )) cos x=±(√(1−sin^2 x)) f(x)_(max) =(√(4 sin x+1))+(√(1−sin^2 x))≈2.663 815 973

$$\frac{{df}\left({x}\right)}{{dx}}=\frac{\mathrm{2}\:\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{4}\:\mathrm{sin}\:{x}+\mathrm{1}}}+\mathrm{sin}\:{x}=\mathrm{0} \\ $$$$\frac{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:{x}}{\:\mathrm{4}\:\mathrm{sin}\:{x}+\mathrm{1}}=\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$$$\frac{\mathrm{4}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}\right)}{\:\mathrm{4}\:\mathrm{sin}\:{x}+\mathrm{1}}=\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$$$\mathrm{4sin}^{\mathrm{3}} \:{x}+\mathrm{5}\:\mathrm{sin}^{\mathrm{2}} \:{x}−\mathrm{4}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{3}} \:{x}}−\frac{\mathrm{5}}{\mathrm{4}\:\mathrm{sin}\:{x}}−\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(−\frac{\mathrm{5}}{\mathrm{12}}\right)^{\mathrm{3}} =\frac{\mathrm{307}}{\mathrm{1728}}>\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{sin}\:{x}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{921}}}{\mathrm{9}}+\mathrm{4}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{921}}}{\mathrm{9}}−\mathrm{4}}\right) \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\frac{\mathrm{2}}{\:\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{921}}}{\mathrm{9}}+\mathrm{4}}−\sqrt[{\mathrm{3}}]{\frac{\sqrt{\mathrm{921}}}{\mathrm{9}}−\mathrm{4}}} \\ $$$$\mathrm{cos}\:{x}=\pm\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}} \\ $$$${f}\left({x}\right)_{{max}} =\sqrt{\mathrm{4}\:\mathrm{sin}\:{x}+\mathrm{1}}+\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}}\approx\mathrm{2}.\mathrm{663}\:\mathrm{815}\:\mathrm{973} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com