Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 114099 by mnjuly1970 last updated on 17/Sep/20

.... mathematical analysis.... prove that :: Σ_(n=1) ^∞ ( ((3^n −1)/4^n ))ζ(n+1) =π m.n.july.1970#

$$\:\:\:....\:\:{mathematical}\:\:{analysis}....\:\: \\ $$$$\:\:{prove}\:{that}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\:\frac{\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{4}^{{n}} }\right)\zeta\left({n}+\mathrm{1}\right)\:=\pi\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}.{n}.{july}.\mathrm{1970}# \\ $$$$ \\ $$

Answered by maths mind last updated on 17/Sep/20

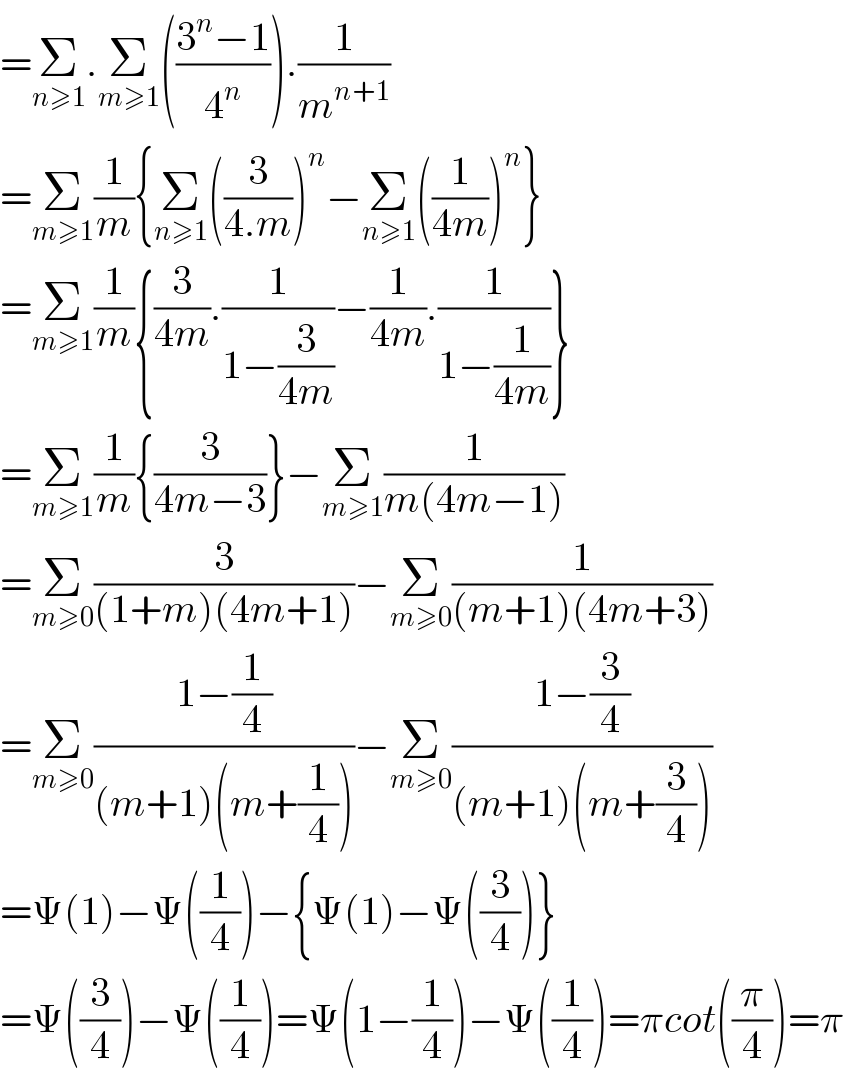
=Σ_(n≥1) .Σ_(m≥1) (((3^n −1)/4^n )).(1/m^(n+1) ) =Σ_(m≥1) (1/m){Σ_(n≥1) ((3/(4.m)))^n −Σ_(n≥1) ((1/(4m)))^n } =Σ_(m≥1) (1/m){(3/(4m)).(1/(1−(3/(4m))))−(1/(4m)).(1/(1−(1/(4m))))} =Σ_(m≥1) (1/m){(3/(4m−3))}−Σ_(m≥1) (1/(m(4m−1))) =Σ_(m≥0) (3/((1+m)(4m+1)))−Σ_(m≥0) (1/((m+1)(4m+3))) =Σ_(m≥0) ((1−(1/4))/((m+1)(m+(1/4))))−Σ_(m≥0) ((1−(3/4))/((m+1)(m+(3/4)))) =Ψ(1)−Ψ((1/4))−{Ψ(1)−Ψ((3/4))} =Ψ((3/4))−Ψ((1/4))=Ψ(1−(1/4))−Ψ((1/4))=πcot((π/4))=π

$$=\underset{{n}\geqslant\mathrm{1}} {\sum}.\underset{{m}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{3}^{{n}} −\mathrm{1}}{\mathrm{4}^{{n}} }\right).\frac{\mathrm{1}}{{m}^{{n}+\mathrm{1}} } \\ $$$$=\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{m}}\left\{\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{3}}{\mathrm{4}.{m}}\right)^{{n}} −\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{4}{m}}\right)^{{n}} \right\} \\ $$$$=\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{m}}\left\{\frac{\mathrm{3}}{\mathrm{4}{m}}.\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}{m}}}−\frac{\mathrm{1}}{\mathrm{4}{m}}.\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}{m}}}\right\} \\ $$$$=\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{m}}\left\{\frac{\mathrm{3}}{\mathrm{4}{m}−\mathrm{3}}\right\}−\underset{{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{m}\left(\mathrm{4}{m}−\mathrm{1}\right)} \\ $$$$=\underset{{m}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{3}}{\left(\mathrm{1}+{m}\right)\left(\mathrm{4}{m}+\mathrm{1}\right)}−\underset{{m}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({m}+\mathrm{1}\right)\left(\mathrm{4}{m}+\mathrm{3}\right)} \\ $$$$=\underset{{m}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}{\left({m}+\mathrm{1}\right)\left({m}+\frac{\mathrm{1}}{\mathrm{4}}\right)}−\underset{{m}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}}{\left({m}+\mathrm{1}\right)\left({m}+\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$$$=\Psi\left(\mathrm{1}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\left\{\Psi\left(\mathrm{1}\right)−\Psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right\} \\ $$$$=\Psi\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\Psi\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\pi{cot}\left(\frac{\pi}{\mathrm{4}}\right)=\pi \\ $$

Commented by mnjuly1970 last updated on 18/Sep/20

thank you sir.grateful...

$${thank}\:{you}\:{sir}.{grateful}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com