
Question Number 4800 by 123456 last updated on 13/Mar/16
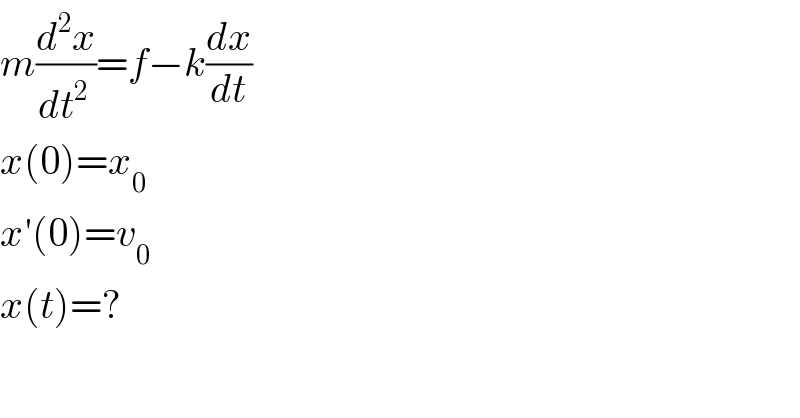
$${m}\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}\:} }={f}−{k}\frac{{dx}}{{dt}} \\ $$$${x}\left(\mathrm{0}\right)={x}_{\mathrm{0}} \\ $$$${x}'\left(\mathrm{0}\right)={v}_{\mathrm{0}} \\ $$$${x}\left({t}\right)=? \\ $$
Answered by Yozzii last updated on 13/Mar/16

$${m}\overset{..} {{x}}+{k}\overset{.} {{x}}−{f}=\mathrm{0} \\ $$$${Auxiliary}\:{quadratic}\:{equation}\:{leads}\:{to} \\ $$$${mp}^{\mathrm{2}} +{kp}−{f}=\mathrm{0} \\ $$$$\Rightarrow{p}=\frac{−{k}\pm\sqrt{{k}^{\mathrm{2}} −\mathrm{4}{m}\left(−{f}\right)}}{\mathrm{2}{m}} \\ $$$${p}=\frac{−{k}\pm\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}}{\mathrm{2}{m}} \\ $$$${If}\:{k}^{\mathrm{2}} +\mathrm{4}{mf}>\mathrm{0}\Rightarrow{p}\:{has}\:{two}\:{distinct}\:{values}. \\ $$$${So},\:{the}\:{general}\:{solution}\:{is}\:{given}\:{by} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\left({t}\right)={Ae}^{{p}_{\mathrm{1}} {t}} +{Be}^{{p}_{\mathrm{2}} {t}} \\ $$$${where}\:{p}_{\mathrm{1}} =\frac{\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}−{k}}{\mathrm{2}{m}}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{p}_{\mathrm{2}} =\frac{−{k}−\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}}{\mathrm{2}{m}}, \\ $$$${A}\:{and}\:{B}\:{are}\:{constants}. \\ $$$${Since}\:{x}\left(\mathrm{0}\right)={x}_{\mathrm{0}} \Rightarrow{x}_{\mathrm{0}} ={A}+{B} \\ $$$$\Rightarrow{A}={x}_{\mathrm{0}} −{B}.......\left(\mathrm{1}\right) \\ $$$${Differentiating}\:{x}\left({t}\right)\:{w}.{r}.{t}\:{t}\:{gives} \\ $$$${x}^{'} \left({t}\right)={Ap}_{\mathrm{1}} {e}^{{p}_{\mathrm{1}} {t}} +{Bp}_{\mathrm{2}} {e}^{{p}_{\mathrm{2}} {t}} \\ $$$${Now},\:{x}^{'} \left(\mathrm{0}\right)={v}_{\mathrm{0}} . \\ $$$$\therefore{v}_{\mathrm{0}} ={Ap}_{\mathrm{1}} +{Bp}_{\mathrm{2}} .........\left(\mathrm{2}\right) \\ $$$${Substituting}\:{A}\:{from}\:\left(\mathrm{1}\right)\:{into}\:\left(\mathrm{2}\right)\:{yields} \\ $$$${v}_{\mathrm{0}} ={p}_{\mathrm{1}} \left({x}_{\mathrm{0}} −{B}\right)+{Bp}_{\mathrm{2}} \\ $$$${v}_{\mathrm{0}} ={p}_{\mathrm{1}} {x}_{\mathrm{0}} +{B}\left({p}_{\mathrm{2}} −{p}_{\mathrm{1}} \right) \\ $$$$\Rightarrow{B}=\frac{{v}_{\mathrm{0}} −{p}_{\mathrm{1}} {x}_{\mathrm{0}} }{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} } \\ $$$${Note}\:{that}\:{p}_{\mathrm{2}} −{p}_{\mathrm{1}} =\frac{−\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}}{{m}}\neq\mathrm{0}\:{unless} \\ $$$${k}^{\mathrm{2}} =−\mathrm{4}{mf}\Rightarrow{mf}\leqslant\mathrm{0}\Rightarrow{k}={m}={f}=\mathrm{0} \\ $$$${or}\:{k}=\pm\mathrm{2}\sqrt{−{mf}}\:{where}\:{mf}<\mathrm{0}.\:{m}\neq\mathrm{0} \\ $$$${since}\:{then}\:{p}_{\mathrm{2}} −{p}_{\mathrm{1}} \:{is}\:{undefined}. \\ $$$${So}\:{k}=\mathrm{0}\:{iff}\:{f}=\mathrm{0}\:{and}\:{m}\neq\mathrm{0}. \\ $$$$\therefore\:{A}={x}_{\mathrm{0}} −\frac{{v}_{\mathrm{0}} −{p}_{\mathrm{1}} {x}_{\mathrm{0}} }{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} }=\frac{{x}_{\mathrm{0}} {p}_{\mathrm{2}} −{v}_{\mathrm{0}} }{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} }. \\ $$$$\therefore\:{x}\left({t}\right)=\left\{\frac{{x}_{\mathrm{0}} {p}_{\mathrm{2}} −{v}_{\mathrm{0}} }{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} }\right\}{e}^{{p}_{\mathrm{1}} {t}} +\left\{\frac{{v}_{\mathrm{0}} −{p}_{\mathrm{1}} {x}_{\mathrm{0}} }{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} }\right\}{e}^{{p}_{\mathrm{2}} {t}} \\ $$$${or}\:{x}\left({t}\right)=\frac{{m}\left({v}_{\mathrm{0}} −{p}_{\mathrm{2}} {x}_{\mathrm{0}} \right){e}^{{p}_{\mathrm{1}} {t}} }{\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}}+\frac{{m}\left({p}_{\mathrm{1}} {x}_{\mathrm{0}} −{v}_{\mathrm{0}} \right){e}^{{p}_{\mathrm{2}} {t}} }{\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}} \\ $$$${or}\:{x}\left({t}\right)=\frac{\mathrm{1}}{\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}}\left(\left\{\frac{\mathrm{2}{v}_{\mathrm{0}} {m}+{x}_{\mathrm{0}} \left({k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}\right)}{\mathrm{2}}\right\}{e}^{{t}\left(\frac{\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}−{k}}{\mathrm{2}{m}}\right)} +\left\{\frac{{x}_{\mathrm{0}} \left(\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}−{k}\right)−\mathrm{2}{mv}_{\mathrm{0}} }{\mathrm{2}}\right\}{e}^{−{t}\left(\frac{{k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{4}{mf}}}{\mathrm{2}{m}}\right)} \right) \\ $$$$ \\ $$$${Checking}: \\ $$$${x}\left(\mathrm{0}\right)=\frac{{x}_{\mathrm{0}} {p}_{\mathrm{2}} −{v}_{\mathrm{0}} }{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} }+\frac{{v}_{\mathrm{0}} −{p}_{\mathrm{1}} {x}_{\mathrm{0}} }{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} }=\frac{{x}_{\mathrm{0}} \left({p}_{\mathrm{2}} −{p}_{\mathrm{1}} \right)}{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} }={x}_{\mathrm{0}} \\ $$$${x}^{'} \left(\mathrm{0}\right)=\frac{\mathrm{1}}{{p}_{\mathrm{2}} −{p}_{\mathrm{1}} }\left({p}_{\mathrm{2}} {p}_{\mathrm{1}} {x}_{\mathrm{0}} −{p}_{\mathrm{1}} {v}_{\mathrm{0}} +{p}_{\mathrm{2}} {v}_{\mathrm{0}} −{p}_{\mathrm{1}} {p}_{\mathrm{2}} {x}_{\mathrm{0}} \right)={v}_{\mathrm{0}} \\ $$$$ \\ $$
Commented by Yozzii last updated on 13/Mar/16
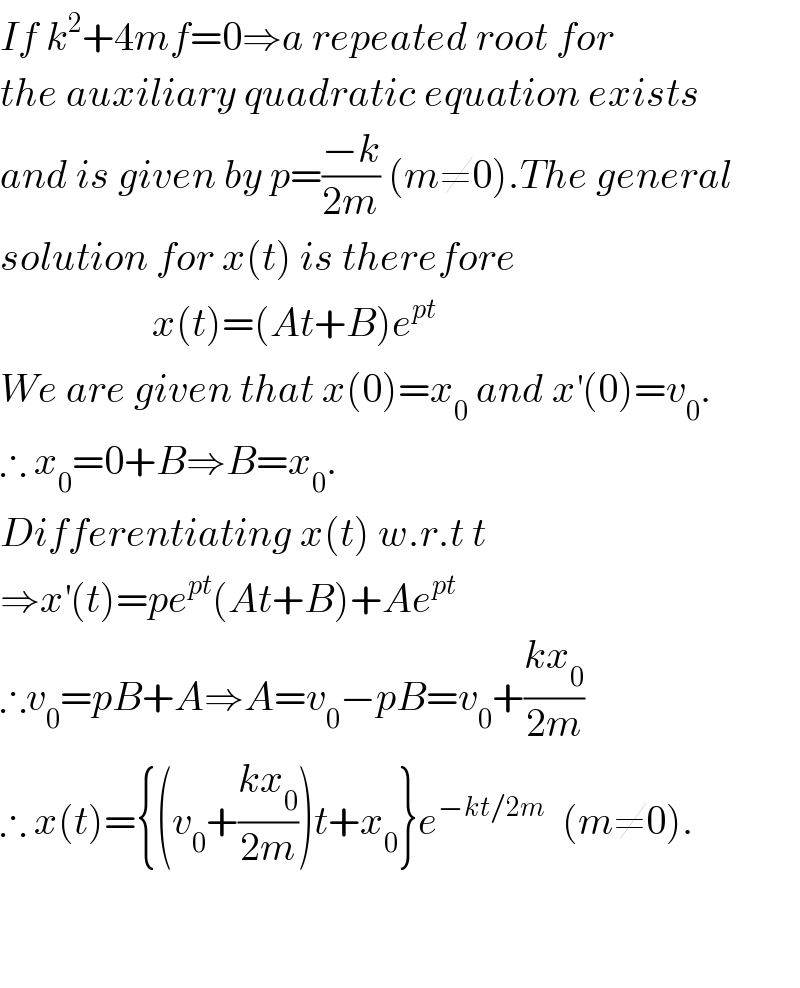
$${If}\:{k}^{\mathrm{2}} +\mathrm{4}{mf}=\mathrm{0}\Rightarrow{a}\:{repeated}\:{root}\:{for} \\ $$$${the}\:{auxiliary}\:{quadratic}\:{equation}\:{exists} \\ $$$${and}\:{is}\:{given}\:{by}\:{p}=\frac{−{k}}{\mathrm{2}{m}}\:\left({m}\neq\mathrm{0}\right).{The}\:{general} \\ $$$${solution}\:{for}\:{x}\left({t}\right)\:{is}\:{therefore} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\left({t}\right)=\left({At}+{B}\right){e}^{{pt}} \\ $$$${We}\:{are}\:{given}\:{that}\:{x}\left(\mathrm{0}\right)={x}_{\mathrm{0}} \:{and}\:{x}^{'} \left(\mathrm{0}\right)={v}_{\mathrm{0}} . \\ $$$$\therefore\:{x}_{\mathrm{0}} =\mathrm{0}+{B}\Rightarrow{B}={x}_{\mathrm{0}} . \\ $$$${Differentiating}\:{x}\left({t}\right)\:{w}.{r}.{t}\:{t} \\ $$$$\Rightarrow{x}^{'} \left({t}\right)={pe}^{{pt}} \left({At}+{B}\right)+{Ae}^{{pt}} \\ $$$$\therefore{v}_{\mathrm{0}} ={pB}+{A}\Rightarrow{A}={v}_{\mathrm{0}} −{pB}={v}_{\mathrm{0}} +\frac{{kx}_{\mathrm{0}} }{\mathrm{2}{m}} \\ $$$$\therefore\:{x}\left({t}\right)=\left\{\left({v}_{\mathrm{0}} +\frac{{kx}_{\mathrm{0}} }{\mathrm{2}{m}}\right){t}+{x}_{\mathrm{0}} \right\}{e}^{−{kt}/\mathrm{2}{m}} \:\:\left({m}\neq\mathrm{0}\right). \\ $$$$ \\ $$$$ \\ $$
Commented by Yozzii last updated on 13/Mar/16
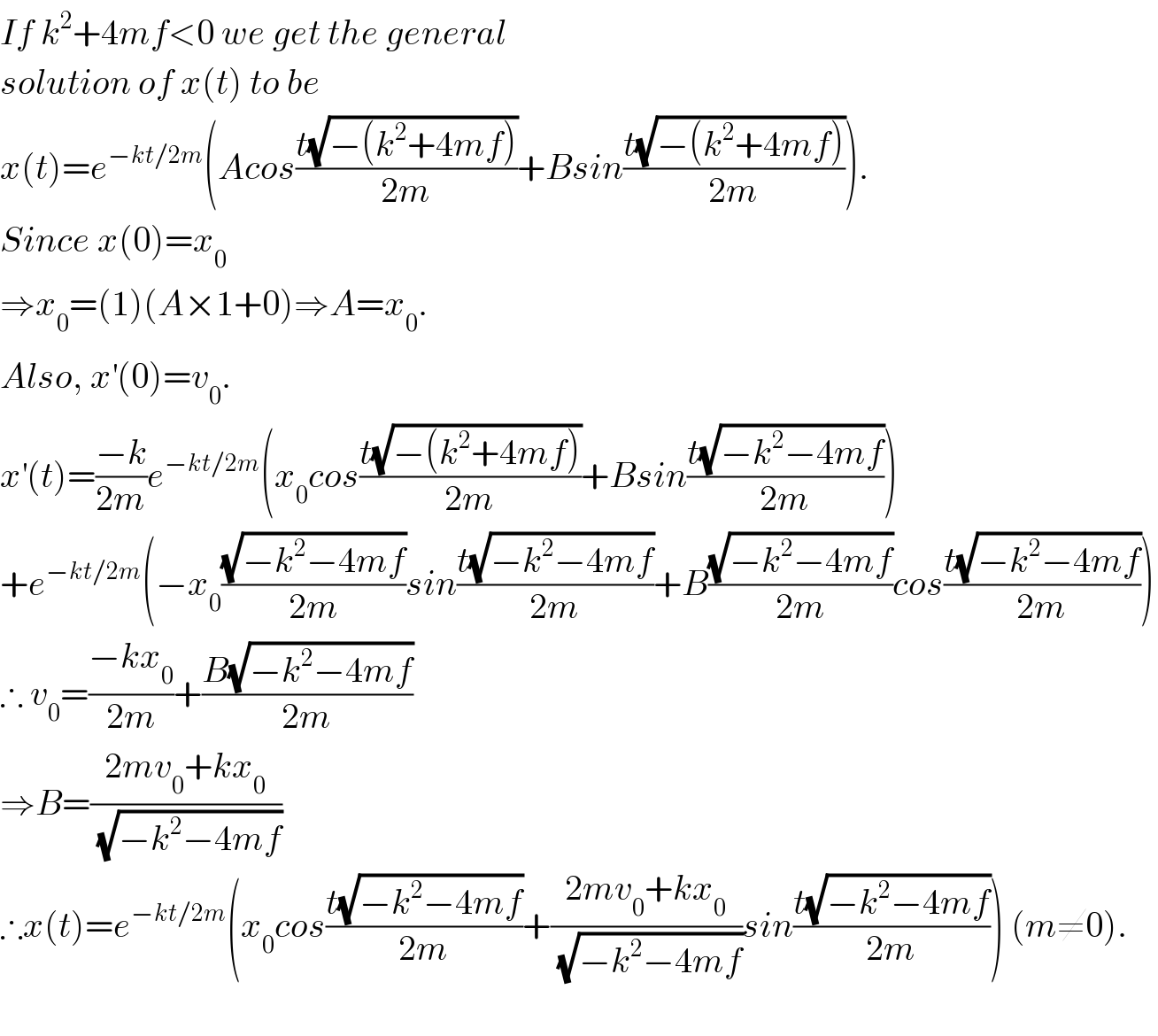
$${If}\:{k}^{\mathrm{2}} +\mathrm{4}{mf}<\mathrm{0}\:{we}\:{get}\:{the}\:{general} \\ $$$${solution}\:{of}\:{x}\left({t}\right)\:{to}\:{be} \\ $$$${x}\left({t}\right)={e}^{−{kt}/\mathrm{2}{m}} \left({Acos}\frac{{t}\sqrt{−\left({k}^{\mathrm{2}} +\mathrm{4}{mf}\right)}}{\mathrm{2}{m}}+{Bsin}\frac{{t}\sqrt{−\left({k}^{\mathrm{2}} +\mathrm{4}{mf}\right)}}{\mathrm{2}{m}}\right). \\ $$$${Since}\:{x}\left(\mathrm{0}\right)={x}_{\mathrm{0}} \: \\ $$$$\Rightarrow{x}_{\mathrm{0}} =\left(\mathrm{1}\right)\left({A}×\mathrm{1}+\mathrm{0}\right)\Rightarrow{A}={x}_{\mathrm{0}} . \\ $$$${Also},\:{x}^{'} \left(\mathrm{0}\right)={v}_{\mathrm{0}} . \\ $$$${x}^{'} \left({t}\right)=\frac{−{k}}{\mathrm{2}{m}}{e}^{−{kt}/\mathrm{2}{m}} \left({x}_{\mathrm{0}} {cos}\frac{{t}\sqrt{−\left({k}^{\mathrm{2}} +\mathrm{4}{mf}\right)}}{\mathrm{2}{m}}+{Bsin}\frac{{t}\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}}{\mathrm{2}{m}}\right) \\ $$$$+{e}^{−{kt}/\mathrm{2}{m}} \left(−{x}_{\mathrm{0}} \frac{\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}}{\mathrm{2}{m}}{sin}\frac{{t}\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}}{\mathrm{2}{m}}+{B}\frac{\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}}{\mathrm{2}{m}}{cos}\frac{{t}\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}}{\mathrm{2}{m}}\right) \\ $$$$\therefore\:{v}_{\mathrm{0}} =\frac{−{kx}_{\mathrm{0}} }{\mathrm{2}{m}}+\frac{{B}\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}}{\mathrm{2}{m}} \\ $$$$\Rightarrow{B}=\frac{\mathrm{2}{mv}_{\mathrm{0}} +{kx}_{\mathrm{0}} }{\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}} \\ $$$$\therefore{x}\left({t}\right)={e}^{−{kt}/\mathrm{2}{m}} \left({x}_{\mathrm{0}} {cos}\frac{{t}\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}}{\mathrm{2}{m}}+\frac{\mathrm{2}{mv}_{\mathrm{0}} +{kx}_{\mathrm{0}} }{\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}}{sin}\frac{{t}\sqrt{−{k}^{\mathrm{2}} −\mathrm{4}{mf}}}{\mathrm{2}{m}}\right)\:\left({m}\neq\mathrm{0}\right). \\ $$$$ \\ $$
Answered by Dnilka228 last updated on 14/Mar/16
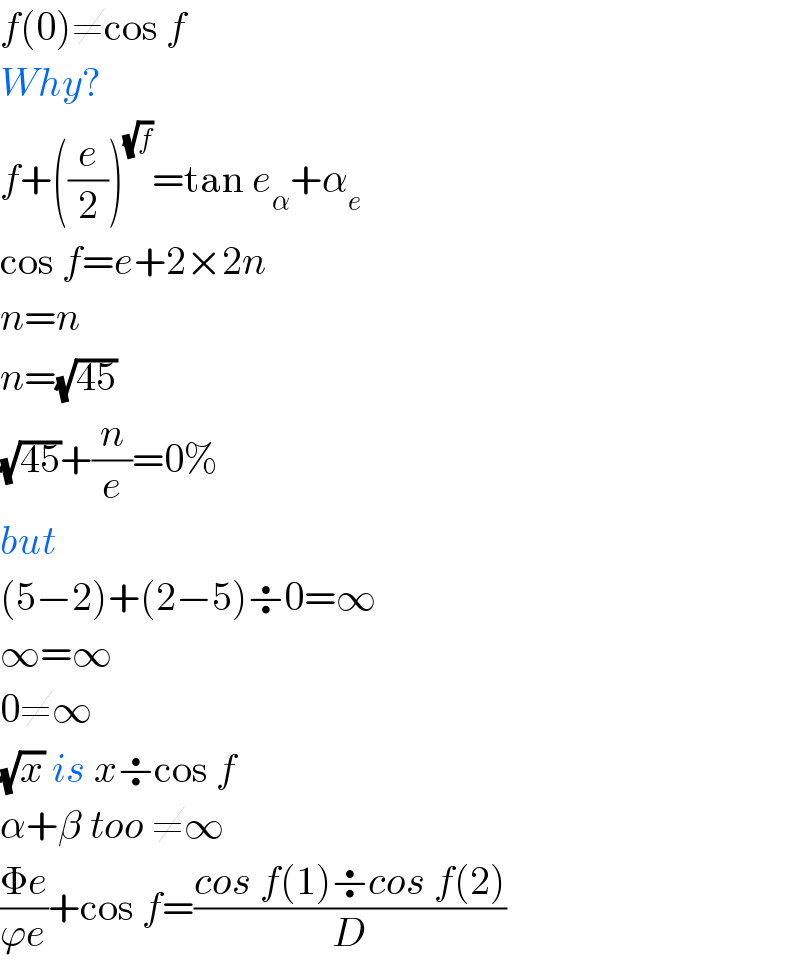
$${f}\left(\mathrm{0}\right)\neq\mathrm{cos}\:{f} \\ $$$${Why}? \\ $$$${f}+\left(\frac{{e}}{\mathrm{2}}\right)^{\sqrt{{f}}} =\mathrm{tan}\:{e}_{\alpha} +\alpha_{{e}} \\ $$$$\mathrm{cos}\:{f}={e}+\mathrm{2}×\mathrm{2}{n} \\ $$$${n}={n} \\ $$$${n}=\sqrt{\mathrm{45}} \\ $$$$\sqrt{\mathrm{45}}+\frac{{n}}{{e}}=\mathrm{0\%} \\ $$$${but} \\ $$$$\left(\mathrm{5}−\mathrm{2}\right)+\left(\mathrm{2}−\mathrm{5}\right)\boldsymbol{\div}\mathrm{0}=\infty \\ $$$$\infty=\infty \\ $$$$\mathrm{0}\neq\infty \\ $$$$\sqrt{{x}}\:{is}\:{x}\boldsymbol{\div}\mathrm{cos}\:{f} \\ $$$$\alpha+\beta\:{too}\:\neq\infty \\ $$$$\frac{\Phi{e}}{\varphi{e}}+\mathrm{cos}\:{f}=\frac{{cos}\:{f}\left(\mathrm{1}\right)\boldsymbol{\div}{cos}\:{f}\left(\mathrm{2}\right)}{{D}} \\ $$
Commented by FilupSmith last updated on 16/Mar/16

$$\infty\neq\infty \\ $$$$\mathrm{Proof}: \\ $$$${a}=\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:...,\:{n}\right\},\:{n}\in\mathbb{N}+\left\{\mathrm{0}\right\},\:\mathrm{0}\leqslant{n}\leqslant\infty \\ $$$${b}=\left\{\mathrm{0},\:\mathrm{0}.\mathrm{01},\:\mathrm{0}.\mathrm{001},\:...,\:\mathrm{0}.\mathrm{2},\:\mathrm{0}.\mathrm{02},\:...,\mathrm{1},\:...,\:{r}\right\},\:{r}\in\mathbb{Z},\:\mathrm{0}\leqslant{r}\leqslant\infty \\ $$$$ \\ $$$$\mathrm{Each}\:\mathrm{set}\:\mathrm{contains}\:\mathrm{all}\:\mathrm{whole}\:\mathrm{numbers}\:\geqslant\mathrm{0}\: \\ $$$$\therefore{a}\subseteq{b} \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{a}\:\mathrm{clear}\:\mathrm{observation}\:\mathrm{that}\:\mid{b}\mid>\mid{a}\mid \\ $$$$\mathrm{So},\:\mathrm{assuming}\:\mathrm{each}\:\mathrm{are}\:\mathrm{infinite},\:{b}\:\mathrm{is}\:\mathrm{still} \\ $$$$\mathrm{bigger}. \\ $$
Commented by FilupSmith last updated on 16/Mar/16
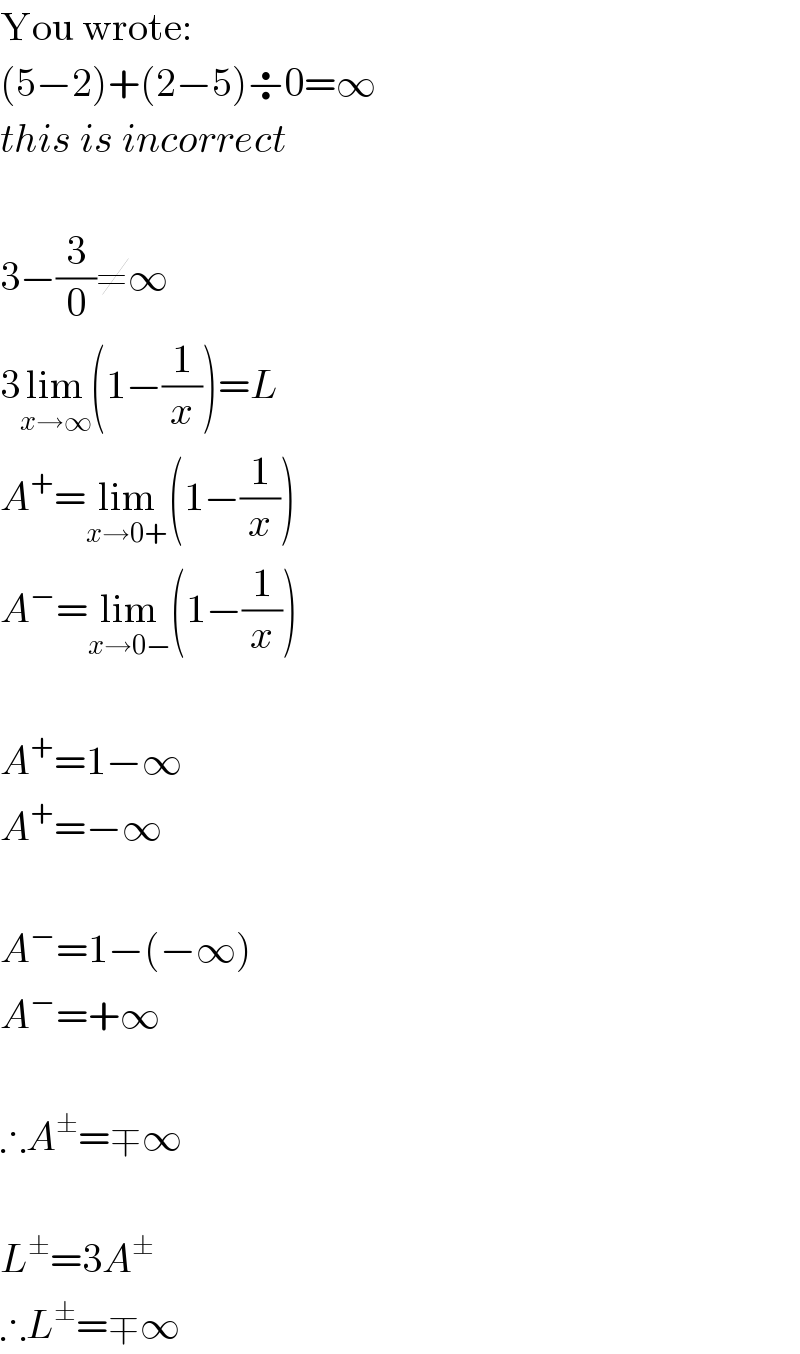
$$\mathrm{You}\:\mathrm{wrote}: \\ $$$$\left(\mathrm{5}−\mathrm{2}\right)+\left(\mathrm{2}−\mathrm{5}\right)\boldsymbol{\div}\mathrm{0}=\infty \\ $$$${this}\:{is}\:{incorrect} \\ $$$$ \\ $$$$\mathrm{3}−\frac{\mathrm{3}}{\mathrm{0}}\neq\infty\: \\ $$$$\mathrm{3}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)={L} \\ $$$${A}^{+} =\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right) \\ $$$${A}^{−} =\underset{{x}\rightarrow\mathrm{0}−} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$ \\ $$$${A}^{+} =\mathrm{1}−\infty \\ $$$${A}^{+} =−\infty \\ $$$$ \\ $$$${A}^{−} =\mathrm{1}−\left(−\infty\right) \\ $$$${A}^{−} =+\infty \\ $$$$ \\ $$$$\therefore{A}^{\pm} =\mp\infty \\ $$$$ \\ $$$${L}^{\pm} =\mathrm{3}{A}^{\pm} \\ $$$$\therefore{L}^{\pm} =\mp\infty \\ $$
