
Question Number 110810 by mohammad17 last updated on 30/Aug/20
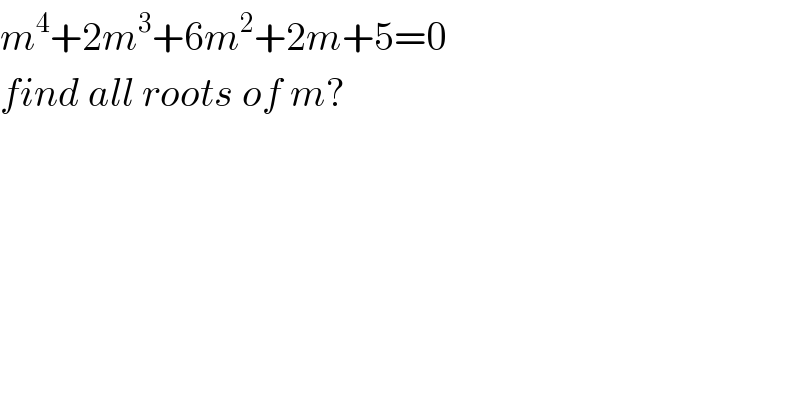
$${m}^{\mathrm{4}} +\mathrm{2}{m}^{\mathrm{3}} +\mathrm{6}{m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{5}=\mathrm{0} \\ $$$${find}\:{all}\:{roots}\:{of}\:{m}? \\ $$
Commented by mohammad17 last updated on 30/Aug/20
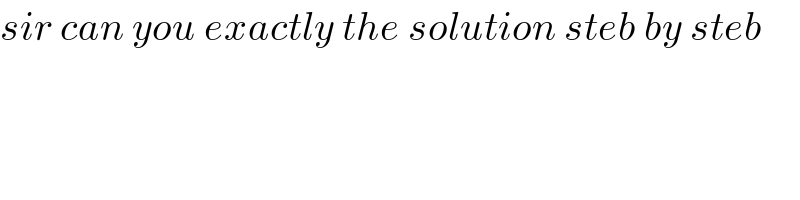
$${sir}\:{can}\:{you}\:{exactly}\:{the}\:{solution}\:{steb}\:{by}\:{steb} \\ $$
Answered by malwan last updated on 31/Aug/20
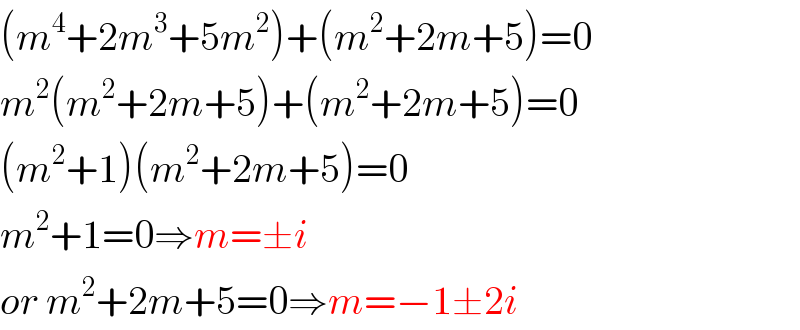
$$\left({m}^{\mathrm{4}} +\mathrm{2}{m}^{\mathrm{3}} +\mathrm{5}{m}^{\mathrm{2}} \right)+\left({m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{5}\right)=\mathrm{0} \\ $$$${m}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{5}\right)+\left({m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{5}\right)=\mathrm{0} \\ $$$$\left({m}^{\mathrm{2}} +\mathrm{1}\right)\left({m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{5}\right)=\mathrm{0} \\ $$$${m}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\Rightarrow{m}=\pm{i} \\ $$$${or}\:{m}^{\mathrm{2}} +\mathrm{2}{m}+\mathrm{5}=\mathrm{0}\Rightarrow{m}=−\mathrm{1}\pm\mathrm{2}{i} \\ $$
Commented by mohammad17 last updated on 31/Aug/20

$${thank}\:{you}\:{sir} \\ $$
Commented by malwan last updated on 31/Aug/20

$${you}\:{welcome} \\ $$
