
Question Number 64541 by Chi Mes Try last updated on 19/Jul/19

$${lol}....{QUESTION}\:{OF}\:\:{THE}\:{DAY} \\ $$$$ \\ $$$${SHOW}\:{FULL}\:{WORKINGS} \\ $$$$ \\ $$$$\int{x}\left(\frac{\left(\mathrm{1}−{x}^{\mathrm{2}} \right){Ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\left(\mathrm{1}−{x}^{\mathrm{2}} \right){Ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}−{x}^{\mathrm{4}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\right){e}^{\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}} {dx} \\ $$
Answered by MJS last updated on 19/Jul/19
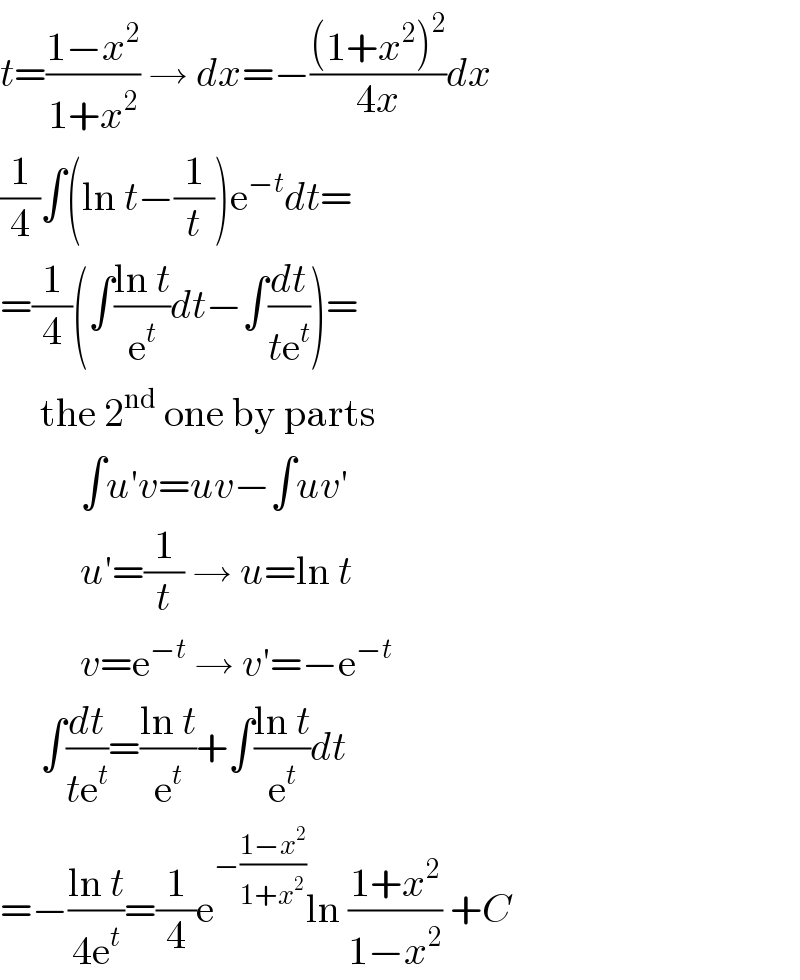
$${t}=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:\rightarrow\:{dx}=−\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}{x}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\left(\mathrm{ln}\:{t}−\frac{\mathrm{1}}{{t}}\right)\mathrm{e}^{−{t}} {dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\int\frac{\mathrm{ln}\:{t}}{\mathrm{e}^{{t}} }{dt}−\int\frac{{dt}}{{t}\mathrm{e}^{{t}} }\right)= \\ $$$$\:\:\:\:\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{one}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\:\:\:\:\:\:\:\:\:\:\int{u}'{v}={uv}−\int{uv}' \\ $$$$\:\:\:\:\:\:\:\:\:\:{u}'=\frac{\mathrm{1}}{{t}}\:\rightarrow\:{u}=\mathrm{ln}\:{t} \\ $$$$\:\:\:\:\:\:\:\:\:\:{v}=\mathrm{e}^{−{t}} \:\rightarrow\:{v}'=−\mathrm{e}^{−{t}} \\ $$$$\:\:\:\:\:\int\frac{{dt}}{{t}\mathrm{e}^{{t}} }=\frac{\mathrm{ln}\:{t}}{\mathrm{e}^{{t}} }+\int\frac{\mathrm{ln}\:{t}}{\mathrm{e}^{{t}} }{dt} \\ $$$$=−\frac{\mathrm{ln}\:{t}}{\mathrm{4e}^{{t}} }=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }} \mathrm{ln}\:\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\:+{C} \\ $$
