
Question Number 151501 by talminator2856791 last updated on 21/Aug/21
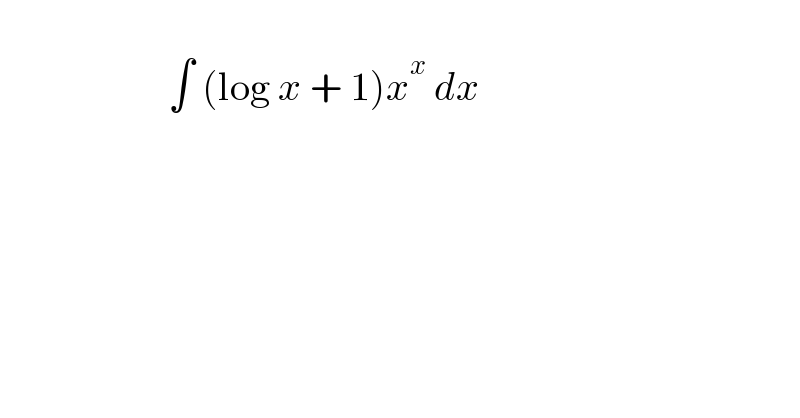
$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\:\left(\mathrm{log}\:{x}\:+\:\mathrm{1}\right){x}^{{x}} \:{dx} \\ $$$$\: \\ $$
Answered by puissant last updated on 21/Aug/21
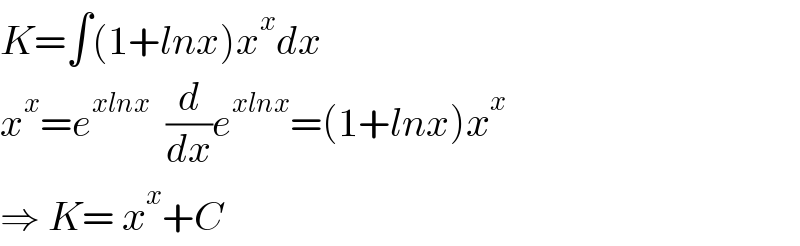
$${K}=\int\left(\mathrm{1}+{lnx}\right){x}^{{x}} {dx} \\ $$$${x}^{{x}} ={e}^{{xlnx}} \:\:\frac{{d}}{{dx}}{e}^{{xlnx}} =\left(\mathrm{1}+{lnx}\right){x}^{{x}} \\ $$$$\Rightarrow\:{K}=\:{x}^{{x}} +{C} \\ $$
Commented by Olaf_Thorendsen last updated on 21/Aug/21
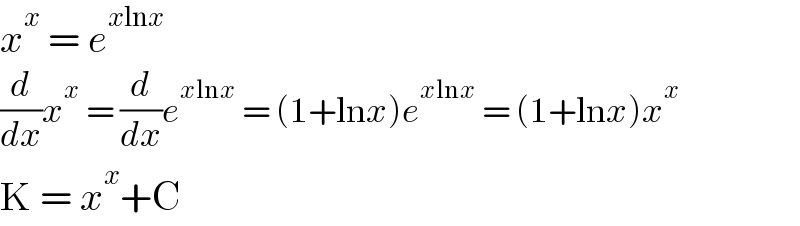
$${x}^{{x}} \:=\:{e}^{{x}\mathrm{ln}{x}} \\ $$$$\frac{{d}}{{dx}}{x}^{{x}} \:=\:\frac{{d}}{{dx}}{e}^{{x}\mathrm{ln}{x}} \:=\:\left(\mathrm{1}+\mathrm{ln}{x}\right){e}^{{x}\mathrm{ln}{x}} \:=\:\left(\mathrm{1}+\mathrm{ln}{x}\right){x}^{{x}} \\ $$$$\mathrm{K}\:=\:{x}^{{x}} +\mathrm{C} \\ $$
Commented by Tawa11 last updated on 22/Aug/21

$$\mathrm{Sir},\:\mathrm{help}\:\mathrm{me}\:\mathrm{check}\:\:\:\:\mathrm{Q151636} \\ $$
