Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 176289 by infinityaction last updated on 15/Sep/22

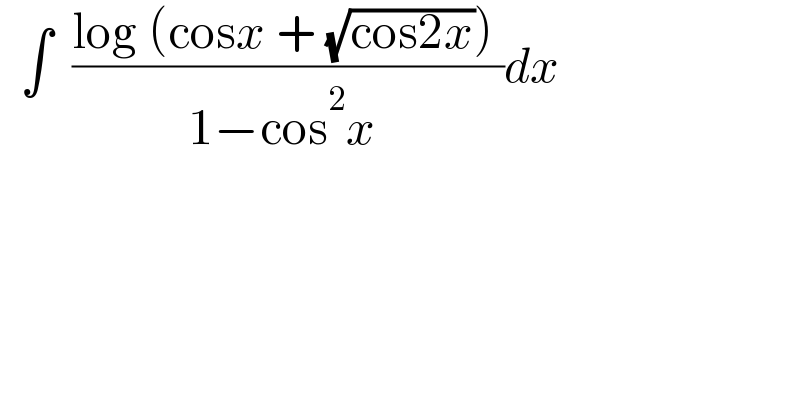
∫ ((log (cosx + (√(cos2x))) )/(1−cos^2 x ))dx

$$\:\:\int\:\:\frac{\mathrm{log}\:\left(\mathrm{cos}{x}\:+\:\sqrt{\mathrm{cos2}{x}}\right)\:}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} {x}\:}{dx} \\ $$

Commented by infinityaction last updated on 16/Sep/22

∫cosec^2 x log[sinx(cotx + (√(cot^2 x−1 )))dx ∫cosec^2 x log(sinx)dx_(Ψ_1 ) +∫log(cotx+(√(cot^2 x−1)))csc^2 xdx_(Ψ_2 ) 𝚿_1 = −log(sinx)cotx−x+∫cot^2 xdx 𝚿_1 = −log(sinx)cotx −x −cotx+c_1 𝚿_2 = ∫log (cotx+(√(cot^2 x−1)))cosec^2 xdx put cotx = t ⇒ −cosec^2 xdx = dt Ψ_1 = −∫log(t +(√(t^2 −1)))dt 𝚿_(2 ) = −tlog(t+(√(t^2 −1)))−∫t.((1+((2t)/(2(√(t^2 −1)))))/(t+(√(t^2 −1))))dt 𝚿_(2 ) = −tlog (t+(√(t^2 −1)))+∫(t/( (√(t^2 −1))))dt 𝚿_2 = −tlog(t+(√(t^2 −1)))+(√(t^2 −1)) 𝚿_2 = −cotxlog(cotx+((√(cos2x))/(sinx )) )+((√(cos2x))/(sinx )) I= ((√(cos2x))/(sinx ))−x−cotx−cotx.log(cotx+(√(cos2x)))+C

$$\int\boldsymbol{\mathrm{cosec}}^{\mathrm{2}} \boldsymbol{{x}}\:\boldsymbol{\mathrm{log}}\left[\boldsymbol{\mathrm{sin}{x}}\left(\boldsymbol{\mathrm{cotx}}\:+\:\sqrt{\boldsymbol{\mathrm{cot}}^{\mathrm{2}} \boldsymbol{{x}}−\mathrm{1}\:}\right)\boldsymbol{\mathrm{dx}}\right. \\ $$$$\underset{\Psi_{\mathrm{1}} } {\underbrace{\int\boldsymbol{\mathrm{cosec}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{sinx}}\right)\boldsymbol{\mathrm{dx}}}}+\underset{\Psi_{\mathrm{2}} } {\underbrace{\int\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{cotx}}+\sqrt{\boldsymbol{\mathrm{cot}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}−\mathrm{1}}\right)\boldsymbol{\mathrm{csc}}^{\mathrm{2}} {x}\boldsymbol{\mathrm{dx}}}} \\ $$$$\boldsymbol{\Psi}_{\mathrm{1}} \:=\:−\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{sin}{x}}\right)\boldsymbol{\mathrm{cot}{x}}−\boldsymbol{{x}}+\int\boldsymbol{\mathrm{cot}}^{\mathrm{2}} \boldsymbol{{xdx}} \\ $$$$\boldsymbol{\Psi}_{\mathrm{1}} \:=\:\:−\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{sin}{x}}\right)\boldsymbol{\mathrm{cot}{x}}\:−\boldsymbol{{x}}\:−\boldsymbol{\mathrm{cot}{x}}+\boldsymbol{{c}}_{\mathrm{1}} \:\:\:\:\:\:\:\: \\ $$$$\boldsymbol{\Psi}_{\mathrm{2}} \:=\:\int\boldsymbol{\mathrm{log}}\:\left(\boldsymbol{\mathrm{cot}{x}}+\sqrt{\boldsymbol{\mathrm{cot}}^{\mathrm{2}} \boldsymbol{{x}}−\mathrm{1}}\right)\boldsymbol{\mathrm{cosec}}^{\mathrm{2}} \boldsymbol{{xdx}} \\ $$$$\:\:\:\boldsymbol{\mathrm{put}}\:\boldsymbol{\mathrm{cotx}}\:\:=\:\:\:\boldsymbol{\mathrm{t}}\:\:\:\Rightarrow\:\:−\boldsymbol{\mathrm{cosec}}^{\mathrm{2}} \boldsymbol{\mathrm{xdx}}\:=\:\boldsymbol{\mathrm{dt}}\:\:\: \\ $$$$\:\:\:\:\:\:\:\Psi_{\mathrm{1}} \:\:\:\:=\:\:\:−\int\mathrm{log}\left({t}\:+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right){dt} \\ $$$$\boldsymbol{\Psi}_{\mathrm{2}\:\:} =\:−{t}\boldsymbol{\mathrm{log}}\left(\boldsymbol{{t}}+\sqrt{\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{1}}\right)−\int\boldsymbol{{t}}.\frac{\mathrm{1}+\frac{\mathrm{2}\boldsymbol{{t}}}{\mathrm{2}\sqrt{\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{1}}}}{\boldsymbol{{t}}+\sqrt{\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{1}}}\boldsymbol{{dt}}\: \\ $$$$\boldsymbol{\Psi}_{\mathrm{2}\:} =\:−\boldsymbol{{t}\mathrm{log}}\:\left(\boldsymbol{{t}}+\sqrt{\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{1}}\right)+\int\frac{\boldsymbol{{t}}}{\:\sqrt{\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{1}}}\boldsymbol{{dt}} \\ $$$$\boldsymbol{\Psi}_{\mathrm{2}} =\:−\boldsymbol{{t}\mathrm{log}}\left(\boldsymbol{{t}}+\sqrt{\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{1}}\right)+\sqrt{\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\boldsymbol{\Psi}_{\mathrm{2}} \:=\:−\boldsymbol{\mathrm{cot}{x}\mathrm{log}}\left(\boldsymbol{\mathrm{cot}{x}}+\frac{\sqrt{\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{{x}}}}{\boldsymbol{\mathrm{sin}{x}}\:}\:\right)+\frac{\sqrt{\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{{x}}}}{\boldsymbol{\mathrm{sin}{x}}\:} \\ $$$$\boldsymbol{{I}}=\:\frac{\sqrt{\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{{x}}}}{\boldsymbol{\mathrm{sin}{x}}\:}−\boldsymbol{{x}}−\boldsymbol{\mathrm{cot}{x}}−\boldsymbol{\mathrm{cot}{x}}.\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{cot}{x}}+\sqrt{\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{{x}}}\right)+\boldsymbol{{C}}\:\:\: \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com