
Question Number 196355 by MATHEMATICSAM last updated on 23/Aug/23
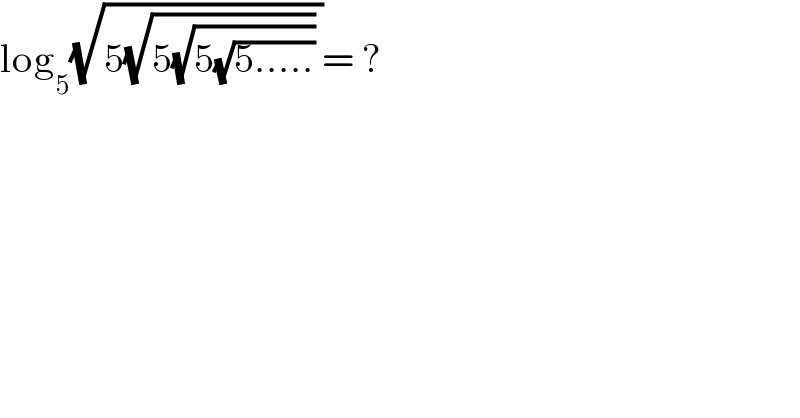
$$\mathrm{log}_{\mathrm{5}} \sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}.....}}}\:}=\:? \\ $$
Commented by bbbbbbbb last updated on 23/Aug/23
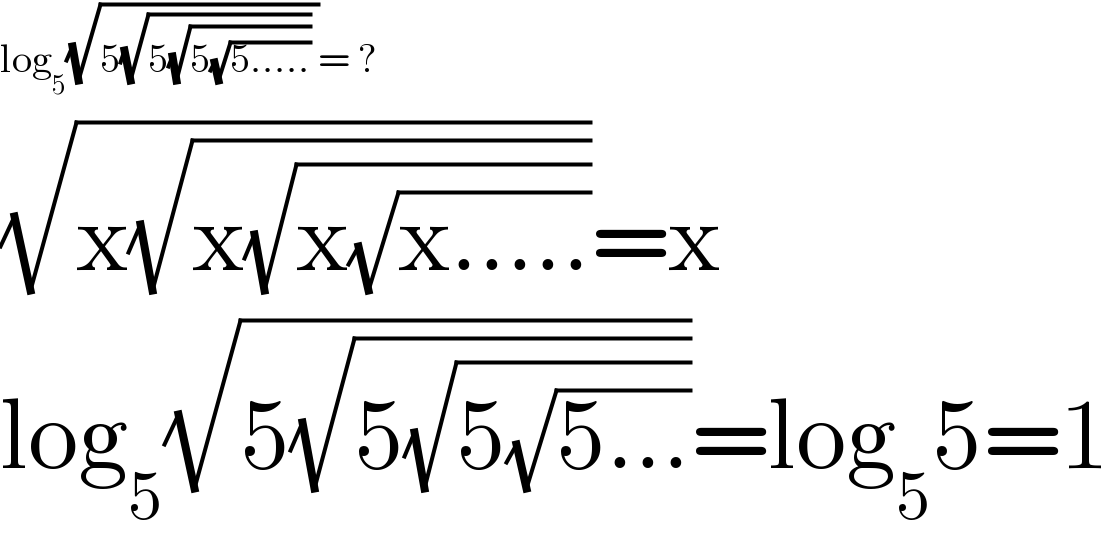
$$\mathrm{log}_{\mathrm{5}} \sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}.....}}}\:}=\:? \\ $$$$\sqrt{\mathrm{x}\sqrt{\mathrm{x}\sqrt{\mathrm{x}\sqrt{\mathrm{x}.....}}}}=\mathrm{x} \\ $$$$\mathrm{log}_{\mathrm{5}} \sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}...}}}}=\mathrm{log}_{\mathrm{5}} \mathrm{5}=\mathrm{1} \\ $$
Answered by som(math1967) last updated on 23/Aug/23
![let (√(5(√(5(√(5...)))))) =x ⇒5(√(5(√(5(√(5...))))))=x^2 ⇒x^2 =5x ∴x=5 [x≠0] log_5 5=1](Q196357.png)
$$\:{let}\:\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}...}}}\:={x} \\ $$$$\Rightarrow\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}...}}}={x}^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{5}{x} \\ $$$$\therefore{x}=\mathrm{5}\:\:\left[{x}\neq\mathrm{0}\right] \\ $$$$\:{log}_{\mathrm{5}} \mathrm{5}=\mathrm{1} \\ $$
Answered by MM42 last updated on 23/Aug/23
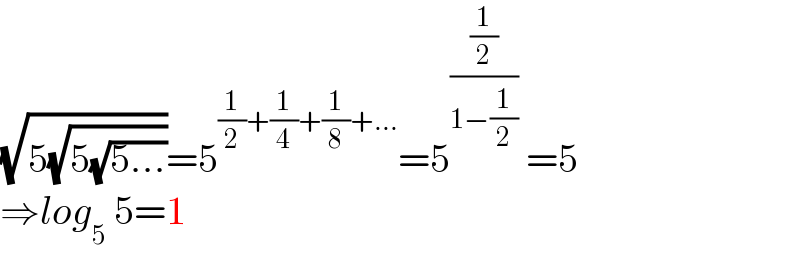
$$\sqrt{\mathrm{5}\sqrt{\mathrm{5}\sqrt{\mathrm{5}...}}}=\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}+...} =\mathrm{5}^{\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}} \:=\mathrm{5} \\ $$$$\Rightarrow{log}_{\mathrm{5}} \:\mathrm{5}=\mathrm{1} \\ $$
