Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 168278 by Florian last updated on 07/Apr/22

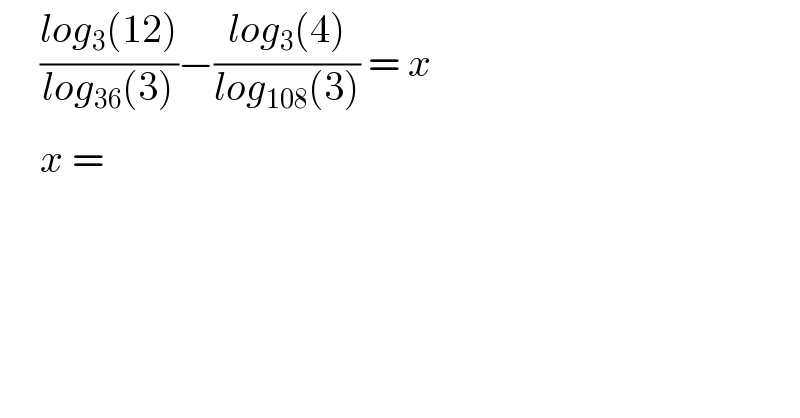
((log_3 (12))/(log_(36) (3)))−((log_3 (4))/(log_(108) (3))) = x x =

$$\:\:\:\:\:\frac{{log}_{\mathrm{3}} \left(\mathrm{12}\right)}{{log}_{\mathrm{36}} \left(\mathrm{3}\right)}−\frac{{log}_{\mathrm{3}} \left(\mathrm{4}\right)}{{log}_{\mathrm{108}} \left(\mathrm{3}\right)}\:=\:{x} \\ $$$$\:\:\:\:\:{x}\:=\: \\ $$

Commented by benhamimed last updated on 07/Apr/22

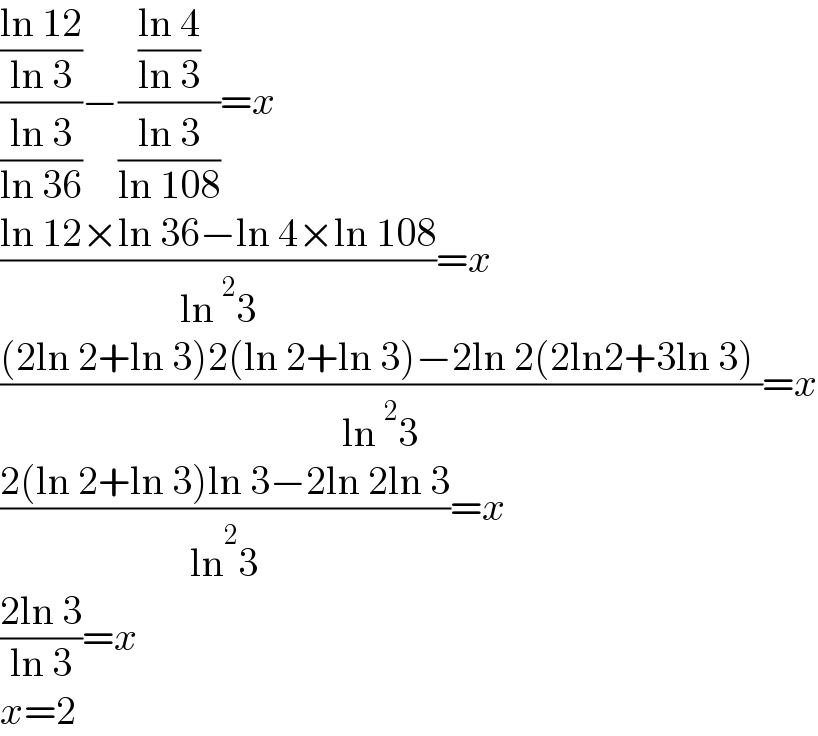
(((ln 12)/(ln 3))/((ln 3)/(ln 36)))−(((ln 4)/(ln 3))/((ln 3)/(ln 108)))=x ((ln 12×ln 36−ln 4×ln 108)/(ln^2 3))=x (((2ln 2+ln 3)2(ln 2+ln 3)−2ln 2(2ln2+3ln 3) )/(ln^2 3))=x ((2(ln 2+ln 3)ln 3−2ln 2ln 3)/(ln ^2 3))=x ((2ln 3)/(ln 3))=x x=2

$$\frac{\frac{\mathrm{ln}\:\mathrm{12}}{\mathrm{ln}\:\mathrm{3}}}{\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{36}}}−\frac{\frac{\mathrm{ln}\:\mathrm{4}}{\mathrm{ln}\:\mathrm{3}}}{\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{108}}}={x} \\ $$$$\frac{\mathrm{ln}\:\mathrm{12}×\mathrm{ln}\:\mathrm{36}−\mathrm{ln}\:\mathrm{4}×\mathrm{ln}\:\mathrm{108}}{\mathrm{ln}\:^{\mathrm{2}} \mathrm{3}}={x} \\ $$$$\frac{\left(\mathrm{2ln}\:\mathrm{2}+\mathrm{ln}\:\mathrm{3}\right)\mathrm{2}\left(\mathrm{ln}\:\mathrm{2}+\mathrm{ln}\:\mathrm{3}\right)−\mathrm{2ln}\:\mathrm{2}\left(\mathrm{2ln2}+\mathrm{3ln}\:\mathrm{3}\right)\:}{\mathrm{ln}\:^{\mathrm{2}} \mathrm{3}}={x} \\ $$$$\frac{\mathrm{2}\left(\mathrm{ln}\:\mathrm{2}+\mathrm{ln}\:\mathrm{3}\right)\mathrm{ln}\:\mathrm{3}−\mathrm{2ln}\:\mathrm{2ln}\:\mathrm{3}}{\mathrm{ln}\overset{\mathrm{2}} {\:}\mathrm{3}}={x} \\ $$$$\frac{\mathrm{2ln}\:\mathrm{3}}{\mathrm{ln}\:\mathrm{3}}={x} \\ $$$${x}=\mathrm{2} \\ $$

Commented by Florian last updated on 07/Apr/22

Very Good !

$${Very}\:{Good}\:! \\ $$

Answered by greogoury55 last updated on 07/Apr/22

⇒x = log _3 (9×4).log _3 (3×4)−log _3 (4).log _3 (27×4) ⇒x=(2+log _3 (4))(1+log _3 (4))−log _3 (4)(3+log _3 (4)) let log _3 (4)= d ⇒x=(2+d)(1+d)−d(3+d) ⇒x=2+3d+d^2 −3d−d^2 ⇒x=2

$$\Rightarrow{x}\:=\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{9}×\mathrm{4}\right).\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{3}×\mathrm{4}\right)−\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{4}\right).\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{27}×\mathrm{4}\right) \\ $$$$\Rightarrow{x}=\left(\mathrm{2}+\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{4}\right)\right)\left(\mathrm{1}+\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{4}\right)\right)−\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{4}\right)\left(\mathrm{3}+\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{4}\right)\right) \\ $$$${let}\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{4}\right)=\:{d} \\ $$$$\Rightarrow{x}=\left(\mathrm{2}+{d}\right)\left(\mathrm{1}+{d}\right)−{d}\left(\mathrm{3}+{d}\right) \\ $$$$\Rightarrow{x}=\mathrm{2}+\mathrm{3}{d}+{d}^{\mathrm{2}} −\mathrm{3}{d}−{d}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com