Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 215840 by golsendro last updated on 19/Jan/25

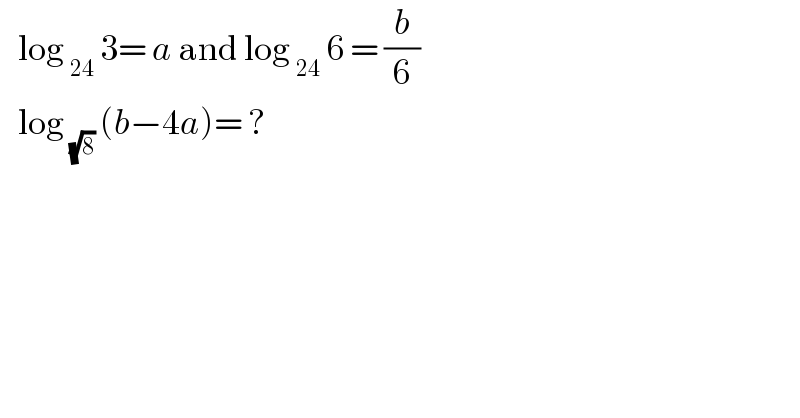
log _(24) 3= a and log _(24) 6 = (b/6) log _(√8) (b−4a)= ?

$$\:\:\:\mathrm{log}\:_{\mathrm{24}} \:\mathrm{3}=\:{a}\:\mathrm{and}\:\mathrm{log}\:_{\mathrm{24}} \:\mathrm{6}\:=\:\frac{{b}}{\mathrm{6}} \\ $$$$\:\:\:\mathrm{log}\:_{\sqrt{\mathrm{8}}} \:\left({b}−\mathrm{4}{a}\right)=\:? \\ $$

Commented by oubiji last updated on 19/Jan/25

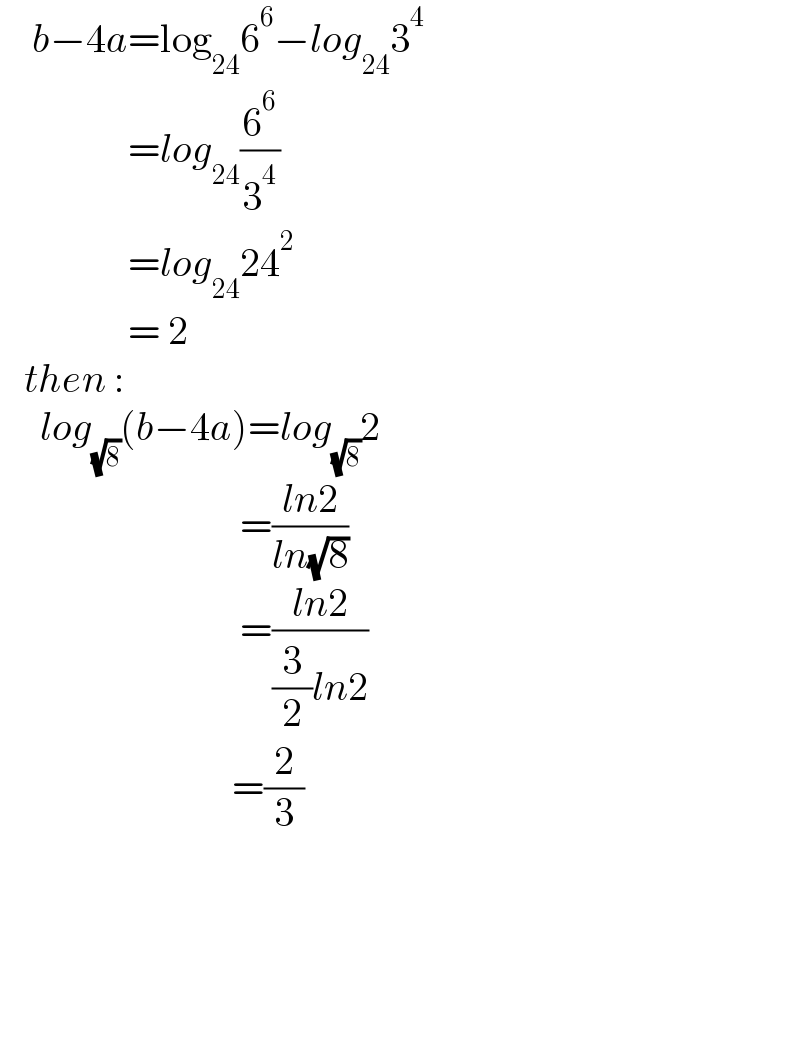
b−4a=log_(24) 6^6 −log_(24) 3^4 =log_(24) (6^6 /3^4 ) =log_(24) 24^2 = 2 then : log_(√8) (b−4a)=log_(√8) 2 =((ln2)/(ln(√8))) =((ln2)/((3/2)ln2)) =(2/3)

$$\:\:\:\:{b}−\mathrm{4}{a}=\mathrm{log}_{\mathrm{24}} \mathrm{6}^{\mathrm{6}} −{log}_{\mathrm{24}} \mathrm{3}^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={log}_{\mathrm{24}} \frac{\mathrm{6}^{\mathrm{6}} }{\mathrm{3}^{\mathrm{4}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={log}_{\mathrm{24}} \mathrm{24}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2} \\ $$$$\:\:\:{then}\:: \\ $$$$\:\:\:\:\:{log}_{\sqrt{\mathrm{8}}} \left({b}−\mathrm{4}{a}\right)={log}_{\sqrt{\mathrm{8}}} \mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{ln}\mathrm{2}}{{ln}\sqrt{\mathrm{8}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{ln}\mathrm{2}}{\frac{\mathrm{3}}{\mathrm{2}}{ln}\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 20/Jan/25

please next time post your solution as “answer” not as a “comment”

$${please}\:{next}\:{time}\:\:{post}\:{your}\:{solution}\:{as}\: \\ $$$$``{answer}''\:{not}\:{as}\:{a}\:``{comment}'' \\ $$

Answered by A5T last updated on 19/Jan/25

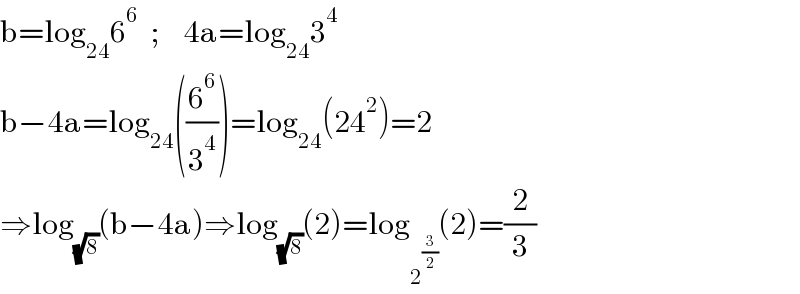
b=log_(24) 6^6 ; 4a=log_(24) 3^4 b−4a=log_(24) ((6^6 /3^4 ))=log_(24) (24^2 )=2 ⇒log_(√8) (b−4a)⇒log_(√8) (2)=log_2^(3/2) (2)=(2/3)

$$\mathrm{b}=\mathrm{log}_{\mathrm{24}} \mathrm{6}^{\mathrm{6}} \:\:;\:\:\:\:\mathrm{4a}=\mathrm{log}_{\mathrm{24}} \mathrm{3}^{\mathrm{4}} \\ $$$$\mathrm{b}−\mathrm{4a}=\mathrm{log}_{\mathrm{24}} \left(\frac{\mathrm{6}^{\mathrm{6}} }{\mathrm{3}^{\mathrm{4}} }\right)=\mathrm{log}_{\mathrm{24}} \left(\mathrm{24}^{\mathrm{2}} \right)=\mathrm{2} \\ $$$$\Rightarrow\mathrm{log}_{\sqrt{\mathrm{8}}} \left(\mathrm{b}−\mathrm{4a}\right)\Rightarrow\mathrm{log}_{\sqrt{\mathrm{8}}} \left(\mathrm{2}\right)=\mathrm{log}_{\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} } \left(\mathrm{2}\right)=\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Answered by MathematicalUser2357 last updated on 26/Jan/25

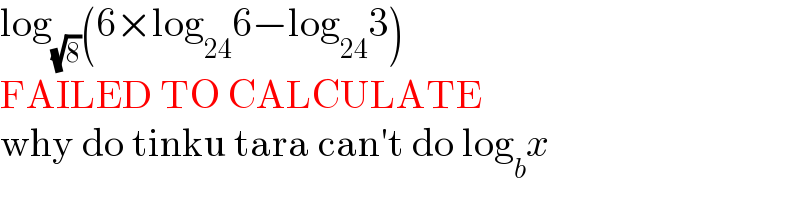
log_(√8) (6×log_(24) 6−log_(24) 3) FAILED TO CALCULATE why do tinku tara can′t do log_b x

$$\mathrm{log}_{\sqrt{\mathrm{8}}} \left(\mathrm{6}×\mathrm{log}_{\mathrm{24}} \mathrm{6}−\mathrm{log}_{\mathrm{24}} \mathrm{3}\right) \\ $$$$\mathrm{FAILED}\:\mathrm{TO}\:\mathrm{CALCULATE} \\ $$$$\mathrm{why}\:\mathrm{do}\:\mathrm{tinku}\:\mathrm{tara}\:\mathrm{can}'\mathrm{t}\:\mathrm{do}\:\mathrm{log}_{{b}} {x} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com