Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 93957 by O Predador last updated on 16/May/20

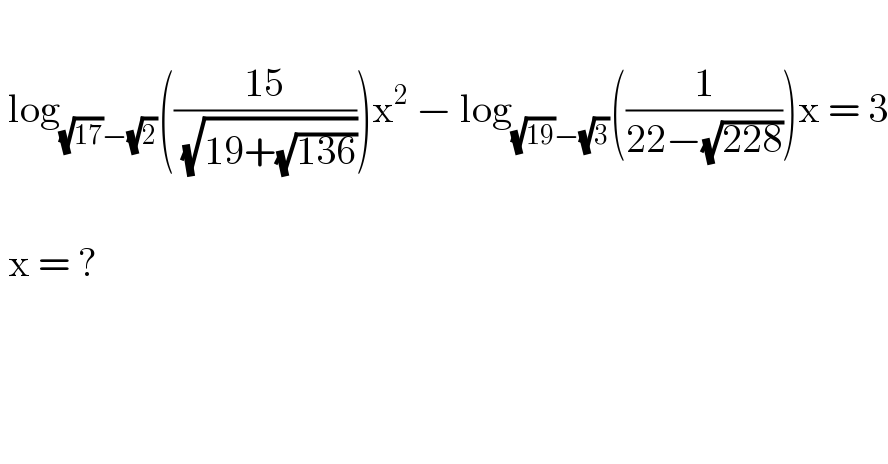
log_((√(17))−(√2)) (((15)/(√(19+(√(136))))))x^2 − log_((√(19))−(√3)) ((1/(22−(√(228)))))x = 3 x = ?

$$\: \\ $$$$\:\mathrm{log}_{\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}} \left(\frac{\mathrm{15}}{\sqrt{\mathrm{19}+\sqrt{\mathrm{136}}}}\right)\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{log}_{\sqrt{\mathrm{19}}−\sqrt{\mathrm{3}}} \left(\frac{\mathrm{1}}{\mathrm{22}−\sqrt{\mathrm{228}}}\right)\mathrm{x}\:=\:\mathrm{3} \\ $$$$\: \\ $$$$\:\mathrm{x}\:=\:? \\ $$

Commented by PRITHWISH SEN 2 last updated on 16/May/20

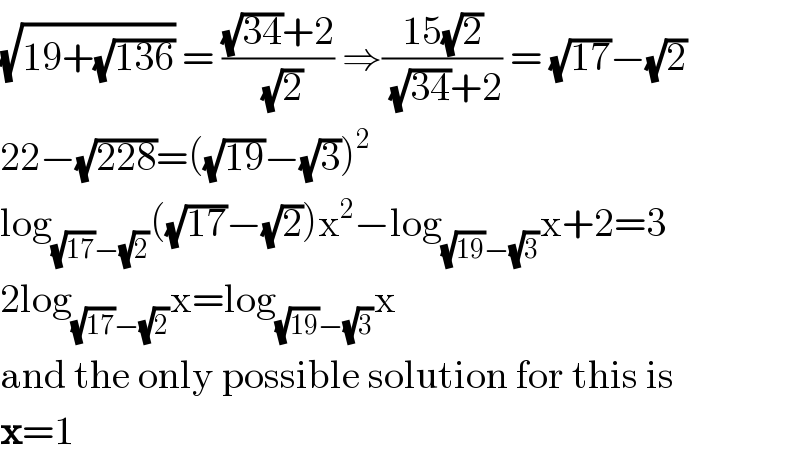
(√(19+(√(136)))) = (((√(34))+2)/(√2)) ⇒((15(√2))/((√(34))+2)) = (√(17))−(√2) 22−(√(228))=((√(19))−(√3))^2 log_((√(17))−(√2)) ((√(17))−(√2))x^2 −log_((√(19))−(√3)) x+2=3 2log_((√(17))−(√2)) x=log_((√(19))−(√3)) x and the only possible solution for this is x=1

$$\sqrt{\mathrm{19}+\sqrt{\mathrm{136}}}\:=\:\frac{\sqrt{\mathrm{34}}+\mathrm{2}}{\sqrt{\mathrm{2}}}\:\Rightarrow\frac{\mathrm{15}\sqrt{\mathrm{2}}}{\sqrt{\mathrm{34}}+\mathrm{2}}\:=\:\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}} \\ $$$$\mathrm{22}−\sqrt{\mathrm{228}}=\left(\sqrt{\mathrm{19}}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\mathrm{log}_{\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}} \left(\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{log}_{\sqrt{\mathrm{19}}−\sqrt{\mathrm{3}}} \mathrm{x}+\mathrm{2}=\mathrm{3} \\ $$$$\mathrm{2log}_{\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}} \mathrm{x}=\mathrm{log}_{\sqrt{\mathrm{19}}−\sqrt{\mathrm{3}}} \mathrm{x} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{only}\:\mathrm{possible}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{this}\:\mathrm{is} \\ $$$$\boldsymbol{\mathrm{x}}=\mathrm{1} \\ $$

Commented by O Predador last updated on 25/May/20

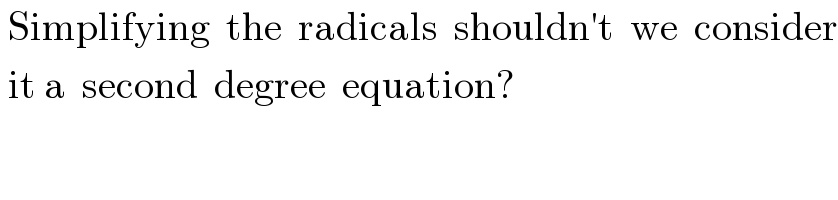
Simplifying the radicals shouldn′t we consider it a second degree equation?

$$\:\mathrm{Simplifying}\:\:\mathrm{the}\:\:\mathrm{radicals}\:\:\mathrm{shouldn}'\mathrm{t}\:\:\mathrm{we}\:\:\mathrm{consider} \\ $$$$\:\mathrm{it}\:\mathrm{a}\:\:\mathrm{second}\:\:\mathrm{degree}\:\:\mathrm{equation}? \\ $$

Commented by O Predador last updated on 25/May/20

Simplificando os radicais na^� o deve-se considerar uma equac_� a^� o do segundo grau?

$$\:\mathrm{Simplificando}\:\:\mathrm{os}\:\:\mathrm{radicais}\:\:\mathrm{n}\bar {\mathrm{a}o}\:\:\mathrm{deve}-\mathrm{se}\:\:\mathrm{considerar} \\ $$$$\:\mathrm{uma}\:\:\mathrm{equa}\underset{} {\mathrm{c}}\bar {\mathrm{a}o}\:\:\mathrm{do}\:\:\mathrm{segundo}\:\:\mathrm{grau}? \\ $$

Commented by PRITHWISH SEN 2 last updated on 25/May/20

English please

$$\mathrm{English}\:\mathrm{please} \\ $$

Commented by PRITHWISH SEN 2 last updated on 25/May/20

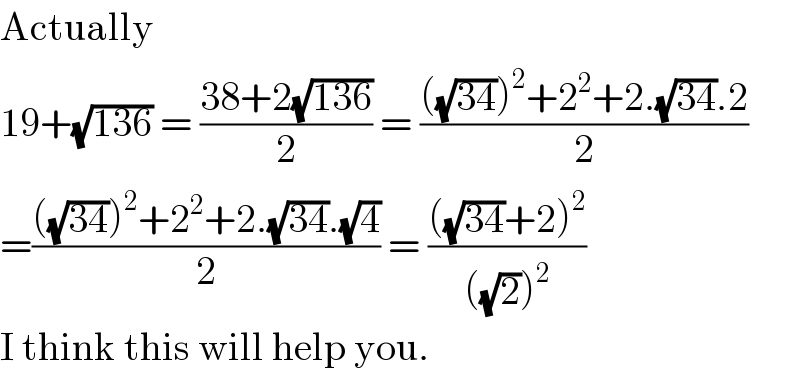
Actually 19+(√(136)) = ((38+2(√(136)))/2) = ((((√(34)))^2 +2^2 +2.(√(34)).2)/2) =((((√(34)))^2 +2^2 +2.(√(34)).(√4))/2) = ((((√(34))+2)^2 )/(((√2))^2 )) I think this will help you.

$$\mathrm{Actually} \\ $$$$\mathrm{19}+\sqrt{\mathrm{136}}\:=\:\frac{\mathrm{38}+\mathrm{2}\sqrt{\mathrm{136}}}{\mathrm{2}}\:=\:\frac{\left(\sqrt{\mathrm{34}}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{2}.\sqrt{\mathrm{34}}.\mathrm{2}}{\mathrm{2}} \\ $$$$=\frac{\left(\sqrt{\mathrm{34}}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{2}.\sqrt{\mathrm{34}}.\sqrt{\mathrm{4}}}{\mathrm{2}}\:=\:\frac{\left(\sqrt{\mathrm{34}}+\mathrm{2}\right)^{\mathrm{2}} }{\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{this}\:\mathrm{will}\:\mathrm{help}\:\mathrm{you}. \\ $$

Commented by O Predador last updated on 26/May/20

Grades: { (((√(19+(√(136)))) = (√(17))+(√2))),((22−(√(228)) = ((√(19))−(√3))^2 )) :} log_((√(17))−(√2)) ((√(17))−(√2))x^2 −log_((√(19))−(√3)) ((1/(((√(19))−(√3))^2 )))x = 3 ... ... x^2 +2x = 3 ... ... x^2 +2x+1 = 3+1 ... ... x+1 = ±2 ... { ((x_1 =−3)),((x_2 =1)) :} Solution: {−3, 1} Wouldn′t that be so?

$$\: \\ $$$$\:\mathrm{Grades}:\:\:\begin{cases}{\sqrt{\mathrm{19}+\sqrt{\mathrm{136}}}\:=\:\sqrt{\mathrm{17}}+\sqrt{\mathrm{2}}}\\{\mathrm{22}−\sqrt{\mathrm{228}}\:=\:\left(\sqrt{\mathrm{19}}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\end{cases} \\ $$$$\: \\ $$$$\:\mathrm{log}_{\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}} \left(\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}\right)\mathrm{x}^{\mathrm{2}} −\mathrm{log}_{\sqrt{\mathrm{19}}−\sqrt{\mathrm{3}}} \left(\frac{\mathrm{1}}{\left(\sqrt{\mathrm{19}}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\right)\mathrm{x}\:=\:\mathrm{3}\:... \\ $$$$\: \\ $$$$\:...\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\:=\:\mathrm{3}\:... \\ $$$$\:...\:\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}\:=\:\mathrm{3}+\mathrm{1}\:... \\ $$$$\:...\:\mathrm{x}+\mathrm{1}\:=\:\pm\mathrm{2}\:... \\ $$$$\: \\ $$$$\:\begin{cases}{\mathrm{x}_{\mathrm{1}} =−\mathrm{3}}\\{\mathrm{x}_{\mathrm{2}} =\mathrm{1}}\end{cases} \\ $$$$\: \\ $$$$\:\mathrm{Solution}:\:\left\{−\mathrm{3},\:\mathrm{1}\right\} \\ $$$$\: \\ $$$$\:\mathrm{Wouldn}'\mathrm{t}\:\:\mathrm{that}\:\:\mathrm{be}\:\:\mathrm{so}? \\ $$

Commented by PRITHWISH SEN 2 last updated on 26/May/20

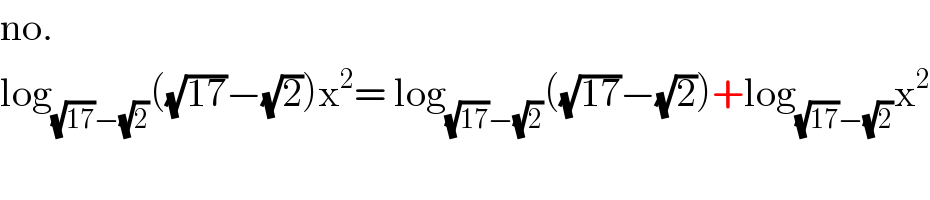
no. log_((√(17))−(√2)) ((√(17))−(√2))x^2 = log_((√(17))−(√2)) ((√(17))−(√2))+log_((√(17))−(√2)) x^2

$$\mathrm{no}. \\ $$$$\mathrm{log}_{\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}} \left(\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}\right)\mathrm{x}^{\mathrm{2}} =\:\mathrm{log}_{\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}} \left(\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}\right)+\mathrm{log}_{\sqrt{\mathrm{17}}−\sqrt{\mathrm{2}}} \mathrm{x}^{\mathrm{2}} \\ $$

Commented by PRITHWISH SEN 2 last updated on 26/May/20

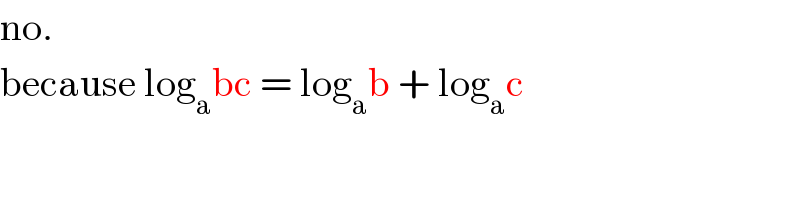
no. because log_a bc = log_a b + log_a c

$$\mathrm{no}. \\ $$$$\mathrm{because}\:\mathrm{log}_{\mathrm{a}} \mathrm{bc}\:=\:\mathrm{log}_{\mathrm{a}} \mathrm{b}\:+\:\mathrm{log}_{\mathrm{a}} \mathrm{c} \\ $$

Commented by O Predador last updated on 26/May/20

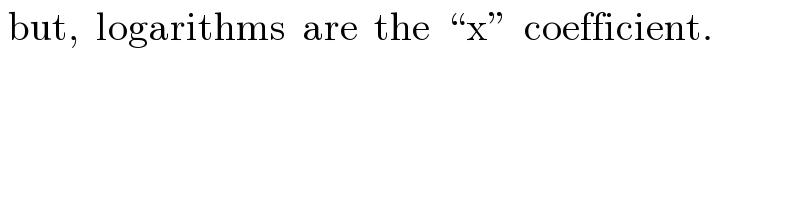
but, logarithms are the “x” coefficient.

$$\:\mathrm{but},\:\:\mathrm{logarithms}\:\:\mathrm{are}\:\:\mathrm{the}\:\:``\mathrm{x}''\:\:\mathrm{coefficient}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com