Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 129451 by bemath last updated on 15/Jan/21

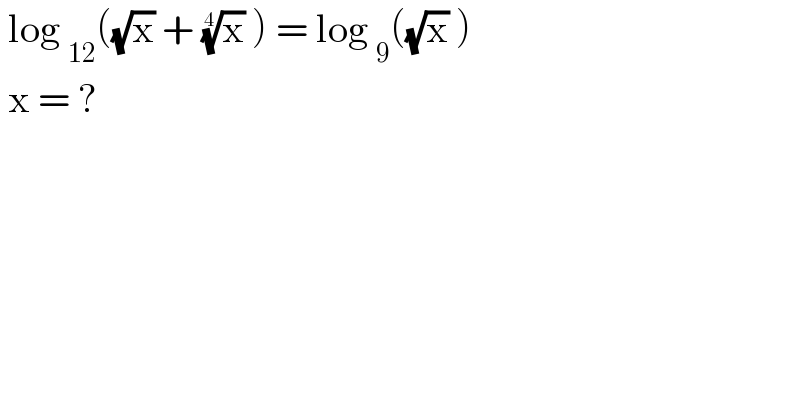
log _(12) ((√x) + (x)^(1/4) ) = log _9 ((√x) ) x = ?

$$\:\mathrm{log}\:_{\mathrm{12}} \left(\sqrt{\mathrm{x}}\:+\:\sqrt[{\mathrm{4}}]{\mathrm{x}}\:\right)\:=\:\mathrm{log}\:_{\mathrm{9}} \left(\sqrt{\mathrm{x}}\:\right)\: \\ $$$$\:\mathrm{x}\:=\:? \\ $$

Answered by liberty last updated on 16/Jan/21

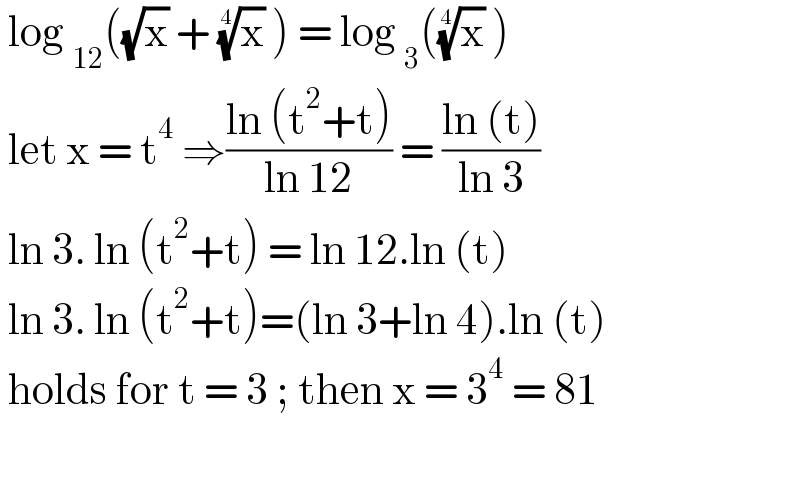
log _(12) ((√x) + (x)^(1/4) ) = log _3 ((x)^(1/4) ) let x = t^4 ⇒((ln (t^2 +t))/(ln 12)) = ((ln (t))/(ln 3)) ln 3. ln (t^2 +t) = ln 12.ln (t) ln 3. ln (t^2 +t)=(ln 3+ln 4).ln (t) holds for t = 3 ; then x = 3^4 = 81

$$\:\mathrm{log}\:_{\mathrm{12}} \left(\sqrt{\mathrm{x}}\:+\:\sqrt[{\mathrm{4}}]{\mathrm{x}}\:\right)\:=\:\mathrm{log}\:_{\mathrm{3}} \left(\sqrt[{\mathrm{4}}]{\mathrm{x}}\:\right) \\ $$$$\:\mathrm{let}\:\mathrm{x}\:=\:\mathrm{t}^{\mathrm{4}} \:\Rightarrow\frac{\mathrm{ln}\:\left(\mathrm{t}^{\mathrm{2}} +\mathrm{t}\right)}{\mathrm{ln}\:\mathrm{12}}\:=\:\frac{\mathrm{ln}\:\left(\mathrm{t}\right)}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\:\mathrm{ln}\:\mathrm{3}.\:\mathrm{ln}\:\left(\mathrm{t}^{\mathrm{2}} +\mathrm{t}\right)\:=\:\mathrm{ln}\:\mathrm{12}.\mathrm{ln}\:\left(\mathrm{t}\right) \\ $$$$\:\mathrm{ln}\:\mathrm{3}.\:\mathrm{ln}\:\left(\mathrm{t}^{\mathrm{2}} +\mathrm{t}\right)=\left(\mathrm{ln}\:\mathrm{3}+\mathrm{ln}\:\mathrm{4}\right).\mathrm{ln}\:\left(\mathrm{t}\right) \\ $$$$\:\mathrm{holds}\:\mathrm{for}\:\mathrm{t}\:=\:\mathrm{3}\:;\:\mathrm{then}\:\mathrm{x}\:=\:\mathrm{3}^{\mathrm{4}} \:=\:\mathrm{81}\: \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com