Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 183594 by greougoury555 last updated on 27/Dec/22

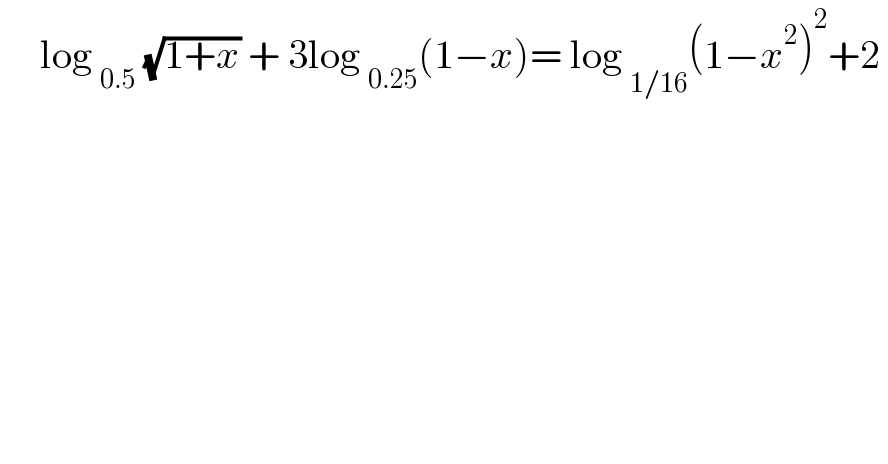
log _(0.5) (√(1+x)) + 3log _(0.25) (1−x)= log _(1/16) (1−x^2 )^2 +2

$$\:\:\:\:\:\mathrm{log}\:_{\mathrm{0}.\mathrm{5}} \:\sqrt{\mathrm{1}+{x}}\:+\:\mathrm{3log}\:_{\mathrm{0}.\mathrm{25}} \left(\mathrm{1}−{x}\right)=\:\mathrm{log}\:_{\mathrm{1}/\mathrm{16}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{2}\: \\ $$

Answered by hmr last updated on 27/Dec/22

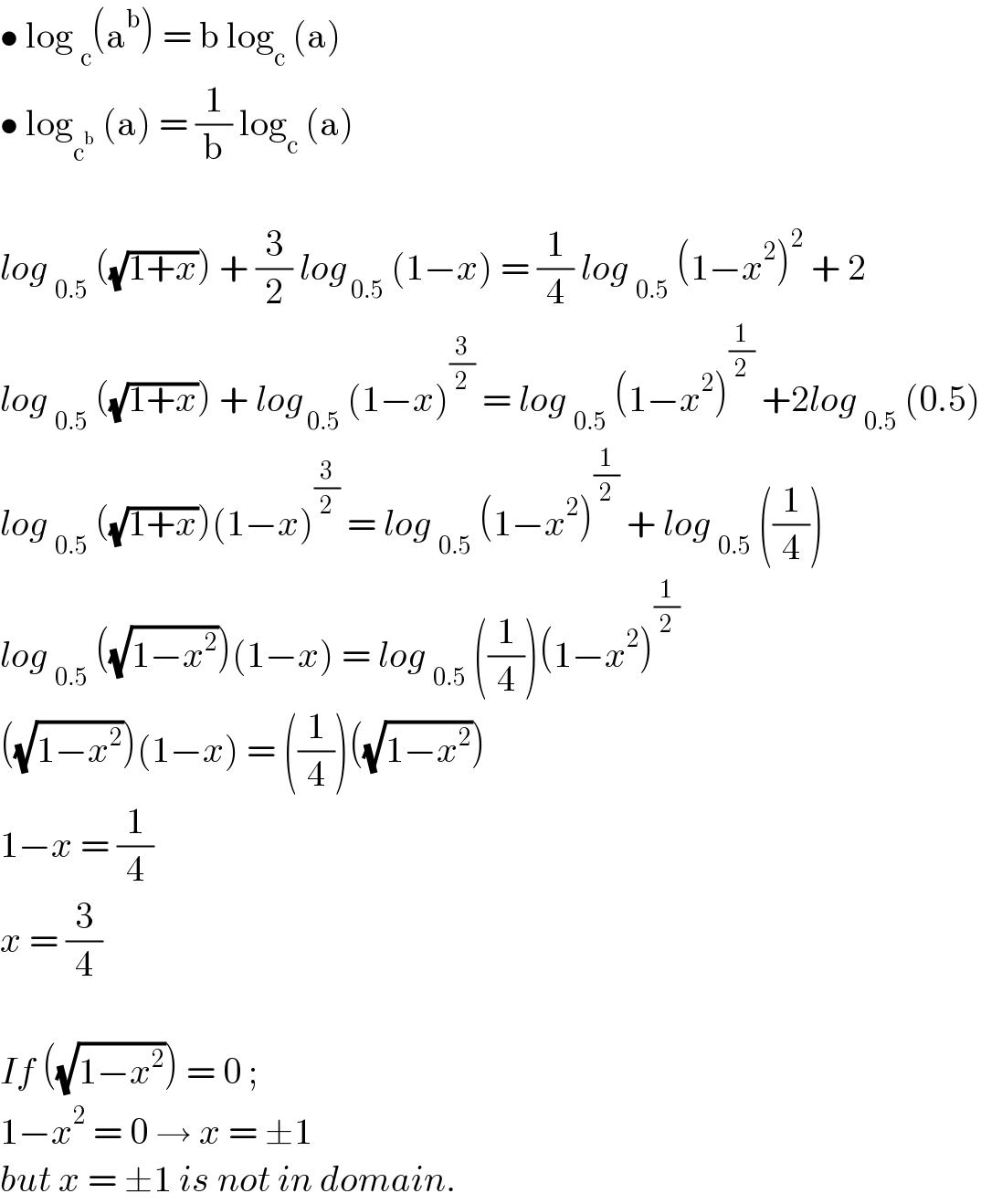
• log _c (a^b ) = b log_c (a) • log_c^b (a) = (1/b) log_c (a) log _(0.5) ((√(1+x))) + (3/2) log_( 0.5) (1−x) = (1/4) log _(0.5) (1−x^2 )^2 + 2 log _(0.5) ((√(1+x))) + log_( 0.5) (1−x)^(3/2) = log _(0.5) (1−x^2 )^(1/2) +2log _(0.5) (0.5) log _(0.5) ((√(1+x)))(1−x)^(3/2) = log _(0.5) (1−x^2 )^(1/2) + log _(0.5) ((1/4)) log _(0.5) ((√(1−x^2 )))(1−x) = log _(0.5) ((1/4))(1−x^2 )^(1/2) ((√(1−x^2 )))(1−x) = ((1/4))((√(1−x^2 ))) 1−x = (1/4) x = (3/4) If ((√(1−x^2 ))) = 0 ; 1−x^2 = 0 → x = ±1 but x = ±1 is not in domain.

$$\bullet\:\mathrm{log}\:_{\mathrm{c}} \left(\mathrm{a}^{\mathrm{b}} \right)\:=\:\mathrm{b}\:\mathrm{log}_{\mathrm{c}} \:\left(\mathrm{a}\right) \\ $$$$\bullet\:\mathrm{log}_{\mathrm{c}^{\mathrm{b}} } \:\left(\mathrm{a}\right)\:=\:\frac{\mathrm{1}}{\mathrm{b}}\:\mathrm{log}_{\mathrm{c}} \:\left(\mathrm{a}\right) \\ $$$$ \\ $$$${log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\sqrt{\mathrm{1}+{x}}\right)\:+\:\frac{\mathrm{3}}{\mathrm{2}}\:{log}_{\:\mathrm{0}.\mathrm{5}} \:\left(\mathrm{1}−{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:{log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\:\mathrm{2} \\ $$$${log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\sqrt{\mathrm{1}+{x}}\right)\:+\:{log}_{\:\mathrm{0}.\mathrm{5}} \:\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:=\:{log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\mathrm{2}{log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\mathrm{0}.\mathrm{5}\right) \\ $$$${log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\sqrt{\mathrm{1}+{x}}\right)\left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:=\:{log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\:{log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$${log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)\left(\mathrm{1}−{x}\right)\:=\:{log}\:_{\mathrm{0}.\mathrm{5}} \:\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)\left(\mathrm{1}−{x}\right)\:=\:\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right) \\ $$$$\mathrm{1}−{x}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${x}\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$$${If}\:\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)\:=\:\mathrm{0}\:;\: \\ $$$$\mathrm{1}−{x}^{\mathrm{2}} \:=\:\mathrm{0}\:\rightarrow\:{x}\:=\:\pm\mathrm{1} \\ $$$${but}\:{x}\:=\:\pm\mathrm{1}\:{is}\:{not}\:{in}\:{domain}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com