
Question Number 101597 by Rio Michael last updated on 03/Jul/20
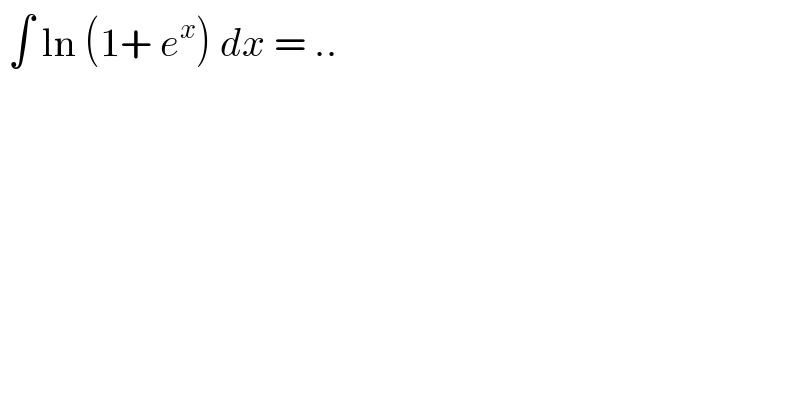
$$\:\int\:\mathrm{ln}\:\left(\mathrm{1}+\:{e}^{{x}} \right)\:{dx}\:=\:.. \\ $$
Commented by Dwaipayan Shikari last updated on 03/Jul/20
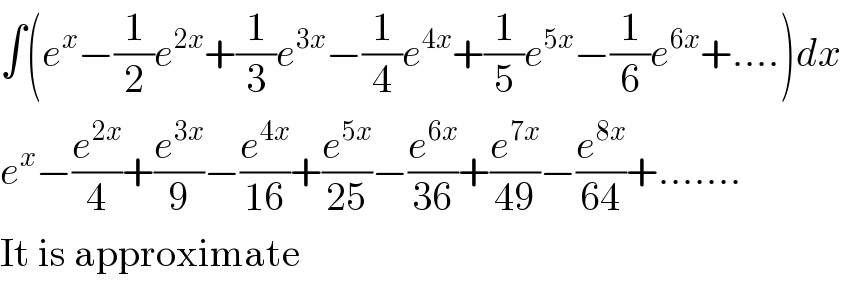
$$\int\left({e}^{{x}} −\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}{x}} +\frac{\mathrm{1}}{\mathrm{3}}{e}^{\mathrm{3}{x}} −\frac{\mathrm{1}}{\mathrm{4}}{e}^{\mathrm{4}{x}} +\frac{\mathrm{1}}{\mathrm{5}}{e}^{\mathrm{5}{x}} −\frac{\mathrm{1}}{\mathrm{6}}{e}^{\mathrm{6}{x}} +....\right){dx} \\ $$$${e}^{{x}} −\frac{{e}^{\mathrm{2}{x}} }{\mathrm{4}}+\frac{{e}^{\mathrm{3}{x}} }{\mathrm{9}}−\frac{{e}^{\mathrm{4}{x}} }{\mathrm{16}}+\frac{{e}^{\mathrm{5}{x}} }{\mathrm{25}}−\frac{{e}^{\mathrm{6}{x}} }{\mathrm{36}}+\frac{{e}^{\mathrm{7}{x}} }{\mathrm{49}}−\frac{{e}^{\mathrm{8}{x}} }{\mathrm{64}}+....... \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{approximate} \\ $$
Commented by floor(10²Eta[1]) last updated on 03/Jul/20
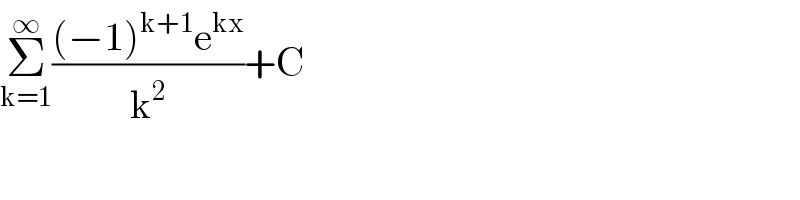
$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}+\mathrm{1}} \mathrm{e}^{\mathrm{kx}} }{\mathrm{k}^{\mathrm{2}} }+\mathrm{C} \\ $$
Commented by Rio Michael last updated on 03/Jul/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
