
Question Number 176379 by doline last updated on 17/Sep/22
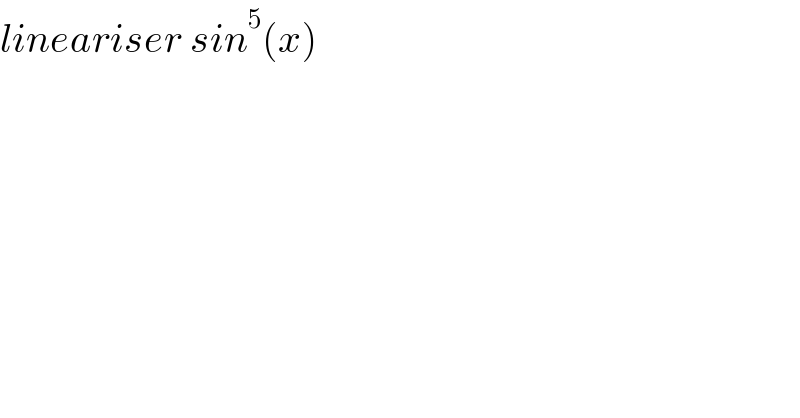
$${lineariser}\:{sin}^{\mathrm{5}} \left({x}\right) \\ $$
Answered by a.lgnaoui last updated on 17/Sep/22
![sin^5 (x)=(((e^(ix) −e^(−ix) )/2))^5 =(1/2^5 )([e^(5ix) −5e^(4ix) e^(−ix) +10e^(3ix) e^(−2ix) −10e^(2ix) e^(−3ix) +5e^(ix) e^(−4ix) −e^(−5ix) ) =(1/2^5 )[(e^(5ix) −5e^(3ix) +10e^(ix) −10e^(−ix) +5e^(−3ix) −e^(−5ix) ) =(1/2^5 )[(e^(5ix) −e^(−5ix) )−5(e^(3ix) −e^(−3ix) )+10(e^(ix) −e^(−ix) )] =(1/2^4 )(sin^5 (x)−5sin^3 (x)+10sin( x)]](Q176381.png)
$$\mathrm{sin}\:^{\mathrm{5}} \left({x}\right)=\left(\frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}}\right)^{\mathrm{5}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\left(\left[{e}^{\mathrm{5}{ix}} −\mathrm{5}{e}^{\mathrm{4}{ix}} {e}^{−{ix}} +\mathrm{10}{e}^{\mathrm{3}{ix}} {e}^{−\mathrm{2}{ix}} −\mathrm{10}{e}^{\mathrm{2}{ix}} {e}^{−\mathrm{3}{ix}} +\mathrm{5}{e}^{{ix}} {e}^{−\mathrm{4}{ix}} −{e}^{−\mathrm{5}{ix}} \right)\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\left[\left({e}^{\mathrm{5}{ix}} −\mathrm{5}{e}^{\mathrm{3}{ix}} +\mathrm{10}{e}^{{ix}} −\mathrm{10}{e}^{−{ix}} +\mathrm{5}{e}^{−\mathrm{3}{ix}} −{e}^{−\mathrm{5}{ix}} \right)\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }\left[\left({e}^{\mathrm{5}{ix}} −{e}^{−\mathrm{5}{ix}} \right)−\mathrm{5}\left({e}^{\mathrm{3}{ix}} −{e}^{−\mathrm{3}{ix}} \right)+\mathrm{10}\left({e}^{{ix}} −{e}^{−{ix}} \right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\left(\mathrm{sin}\:^{\mathrm{5}} \left({x}\right)−\mathrm{5sin}\:^{\mathrm{3}} \left({x}\right)+\mathrm{10sin}\left(\:{x}\right)\right] \\ $$
