Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 185374 by Mastermind last updated on 20/Jan/23

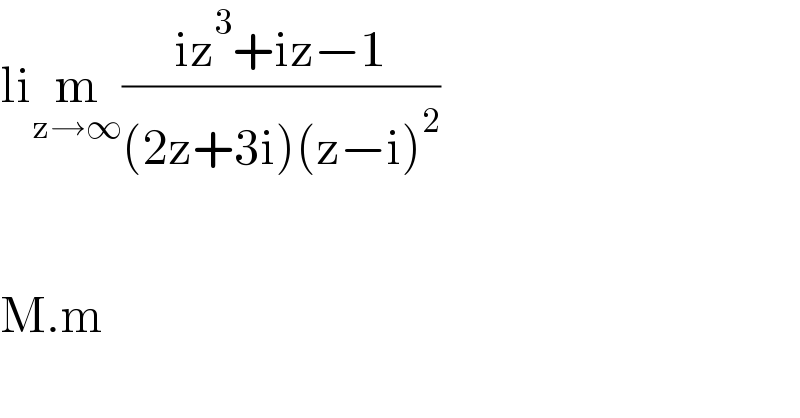
lim_(z→∞) ((iz^3 +iz−1)/((2z+3i)(z−i)^2 )) M.m

$$\mathrm{li}\underset{\mathrm{z}\rightarrow\infty} {\mathrm{m}}\frac{\mathrm{iz}^{\mathrm{3}} +\mathrm{iz}−\mathrm{1}}{\left(\mathrm{2z}+\mathrm{3i}\right)\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Answered by MJS_new last updated on 20/Jan/23

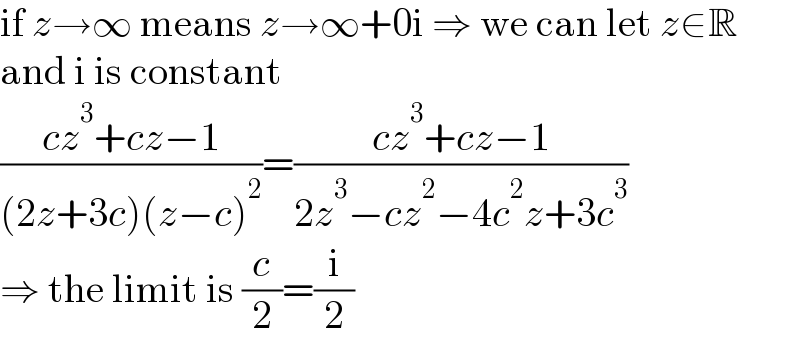
if z→∞ means z→∞+0i ⇒ we can let z∈R and i is constant ((cz^3 +cz−1)/((2z+3c)(z−c)^2 ))=((cz^3 +cz−1)/(2z^3 −cz^2 −4c^2 z+3c^3 )) ⇒ the limit is (c/2)=(i/2)

$$\mathrm{if}\:{z}\rightarrow\infty\:\mathrm{means}\:{z}\rightarrow\infty+\mathrm{0i}\:\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{let}\:{z}\in\mathbb{R} \\ $$$$\mathrm{and}\:\mathrm{i}\:\mathrm{is}\:\mathrm{constant} \\ $$$$\frac{{cz}^{\mathrm{3}} +{cz}−\mathrm{1}}{\left(\mathrm{2}{z}+\mathrm{3}{c}\right)\left({z}−{c}\right)^{\mathrm{2}} }=\frac{{cz}^{\mathrm{3}} +{cz}−\mathrm{1}}{\mathrm{2}{z}^{\mathrm{3}} −{cz}^{\mathrm{2}} −\mathrm{4}{c}^{\mathrm{2}} {z}+\mathrm{3}{c}^{\mathrm{3}} } \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{limit}\:\mathrm{is}\:\frac{{c}}{\mathrm{2}}=\frac{\mathrm{i}}{\mathrm{2}} \\ $$

Commented by Mastermind last updated on 21/Jan/23

Thank you so much boss

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{boss} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com