Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 64539 by mmkkmm000m last updated on 19/Jul/19

lim_(xat 0) [cos^2 (4x)]/x^2 −lim_(x at 0) [cos^3 (6x)]/x^2

$${lim}_{{xat}\:\mathrm{0}} \left[{cos}^{\mathrm{2}} \left(\mathrm{4}{x}\right)\right]/{x}^{\mathrm{2}} \:\:−{lim}_{{x}\:{at}\:\mathrm{0}} \left[{cos}^{\mathrm{3}} \left(\mathrm{6}{x}\right)\right]/{x}^{\mathrm{2}} \\ $$

Commented by kaivan.ahmadi last updated on 19/Jul/19

lim_(x→0) (([cos^2 4x])/x^2 )−lim_(x→0) (([cos^3 6x])/x^2 )= lim_(x→0 ) (([cos^2 4x]−[cos^3 6x])/x^2 )=(([1^− ]−[1^− ])/0^+ )=((0−0)/0^+ )=(0/0^+ )=0

$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\left[{cos}^{\mathrm{2}} \mathrm{4}{x}\right]}{{x}^{\mathrm{2}} }−{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\left[{cos}^{\mathrm{3}} \mathrm{6}{x}\right]}{{x}^{\mathrm{2}} }= \\ $$$${lim}_{{x}\rightarrow\mathrm{0}\:\:} \frac{\left[{cos}^{\mathrm{2}} \mathrm{4}{x}\right]−\left[{cos}^{\mathrm{3}} \mathrm{6}{x}\right]}{{x}^{\mathrm{2}} }=\frac{\left[\mathrm{1}^{−} \right]−\left[\mathrm{1}^{−} \right]}{\mathrm{0}^{+} }=\frac{\mathrm{0}−\mathrm{0}}{\mathrm{0}^{+} }=\frac{\mathrm{0}}{\mathrm{0}^{+} }=\mathrm{0} \\ $$

Commented by MJS last updated on 19/Jul/19

(0/0)≠0

$$\frac{\mathrm{0}}{\mathrm{0}}\neq\mathrm{0} \\ $$

Commented by mathmax by abdo last updated on 19/Jul/19

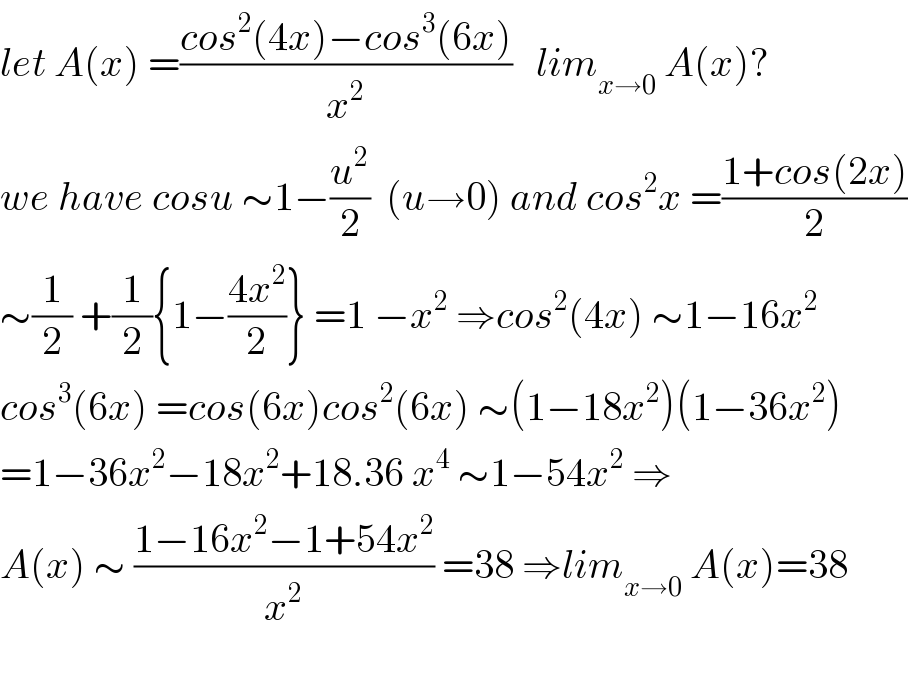
let A(x) =((cos^2 (4x)−cos^3 (6x))/x^2 ) lim_(x→0) A(x)? we have cosu ∼1−(u^2 /2) (u→0) and cos^2 x =((1+cos(2x))/2) ∼(1/2) +(1/2){1−((4x^2 )/2)} =1 −x^2 ⇒cos^2 (4x) ∼1−16x^2 cos^3 (6x) =cos(6x)cos^2 (6x) ∼(1−18x^2 )(1−36x^2 ) =1−36x^2 −18x^2 +18.36 x^4 ∼1−54x^2 ⇒ A(x) ∼ ((1−16x^2 −1+54x^2 )/x^2 ) =38 ⇒lim_(x→0) A(x)=38

$${let}\:{A}\left({x}\right)\:=\frac{{cos}^{\mathrm{2}} \left(\mathrm{4}{x}\right)−{cos}^{\mathrm{3}} \left(\mathrm{6}{x}\right)}{{x}^{\mathrm{2}} }\:\:\:{lim}_{{x}\rightarrow\mathrm{0}} \:{A}\left({x}\right)? \\ $$$${we}\:{have}\:{cosu}\:\sim\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:\:\left({u}\rightarrow\mathrm{0}\right)\:{and}\:{cos}^{\mathrm{2}} {x}\:=\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}} \\ $$$$\sim\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{1}−\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{2}}\right\}\:=\mathrm{1}\:−{x}^{\mathrm{2}} \:\Rightarrow{cos}^{\mathrm{2}} \left(\mathrm{4}{x}\right)\:\sim\mathrm{1}−\mathrm{16}{x}^{\mathrm{2}} \\ $$$${cos}^{\mathrm{3}} \left(\mathrm{6}{x}\right)\:={cos}\left(\mathrm{6}{x}\right){cos}^{\mathrm{2}} \left(\mathrm{6}{x}\right)\:\sim\left(\mathrm{1}−\mathrm{18}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{36}{x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{1}−\mathrm{36}{x}^{\mathrm{2}} −\mathrm{18}{x}^{\mathrm{2}} +\mathrm{18}.\mathrm{36}\:{x}^{\mathrm{4}} \:\sim\mathrm{1}−\mathrm{54}{x}^{\mathrm{2}} \:\Rightarrow \\ $$$${A}\left({x}\right)\:\sim\:\frac{\mathrm{1}−\mathrm{16}{x}^{\mathrm{2}} −\mathrm{1}+\mathrm{54}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:=\mathrm{38}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{A}\left({x}\right)=\mathrm{38} \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 19/Jul/19

(0/ε)=0

$$\frac{\mathrm{0}}{\varepsilon}=\mathrm{0} \\ $$

Commented by kaivan.ahmadi last updated on 19/Jul/19

sir [ ] means integer part

$${sir}\:\left[\:\right]\:{means}\:{integer}\:{part} \\ $$

Commented by mathmax by abdo last updated on 19/Jul/19

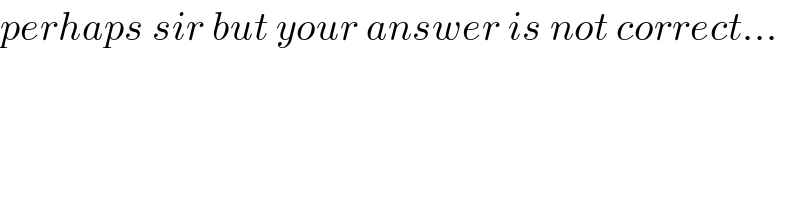
perhaps sir but your answer is not correct...

$${perhaps}\:{sir}\:{but}\:{your}\:{answer}\:{is}\:{not}\:{correct}... \\ $$

Commented by kaivan.ahmadi last updated on 19/Jul/19

why?

$${why}? \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 19/Jul/19

(0/0) is undefined

$$\frac{\mathrm{0}}{\mathrm{0}}\:{is}\:{undefined}\: \\ $$

Commented by MJS last updated on 19/Jul/19

lim_(x→0) [cos^2 4x]=0 lim_(x→0) [cos^3 6x]=0 I think that in this case the difference of the given limits is undefined

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\mathrm{cos}^{\mathrm{2}} \:\mathrm{4}{x}\right]=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\mathrm{cos}^{\mathrm{3}} \:\mathrm{6}{x}\right]=\mathrm{0} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{that}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{the}\:\mathrm{difference}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{given}\:\mathrm{limits}\:\mathrm{is}\:\mathrm{undefined} \\ $$

Answered by MJS last updated on 19/Jul/19

lim_(x→0) ((cos^2 4x −cos^3 6x)/x^2 ) = =lim_(x→0) ((2−cos 18x +2cos 8x −3cos 6x)/(4x^2 )) =lim_(x→0) (((d^2 /dx^2 )[2−cos 18x +2cos 8x −3cos 6x])/((d^2 /dx^2 )[4x^2 ])) = =(1/2)lim_(x→0) (81cos 18x −32cos 8x+27cos 6x)= =38

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}^{\mathrm{2}} \:\mathrm{4}{x}\:−\mathrm{cos}^{\mathrm{3}} \:\mathrm{6}{x}}{{x}^{\mathrm{2}} }\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{cos}\:\mathrm{18}{x}\:+\mathrm{2cos}\:\mathrm{8}{x}\:−\mathrm{3cos}\:\mathrm{6}{x}}{\mathrm{4}{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left[\mathrm{2}−\mathrm{cos}\:\mathrm{18}{x}\:+\mathrm{2cos}\:\mathrm{8}{x}\:−\mathrm{3cos}\:\mathrm{6}{x}\right]}{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left[\mathrm{4}{x}^{\mathrm{2}} \right]}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{81cos}\:\mathrm{18}{x}\:−\mathrm{32cos}\:\mathrm{8}{x}+\mathrm{27cos}\:\mathrm{6}{x}\right)= \\ $$$$=\mathrm{38} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com