
Question Number 122235 by benjo_mathlover last updated on 15/Nov/20
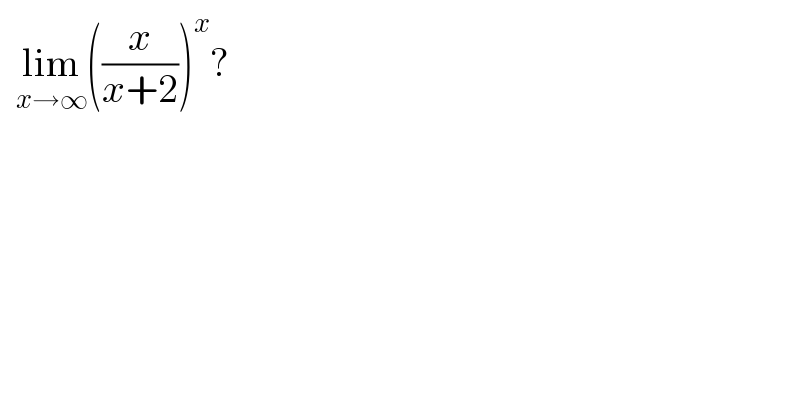
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{x}}{{x}+\mathrm{2}}\right)^{{x}} ?\: \\ $$
Answered by liberty last updated on 15/Nov/20
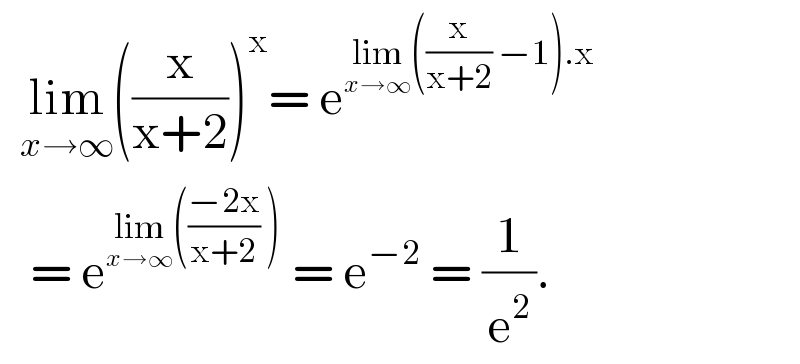
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{x}}{\mathrm{x}+\mathrm{2}}\right)^{\mathrm{x}} =\:\mathrm{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{x}}{\mathrm{x}+\mathrm{2}}\:−\mathrm{1}\right).\mathrm{x}} \\ $$$$\:\:\:=\:\mathrm{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{−\mathrm{2x}}{\mathrm{x}+\mathrm{2}}\:\right)} \:=\:\mathrm{e}^{−\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} }. \\ $$
Answered by Dwaipayan Shikari last updated on 15/Nov/20
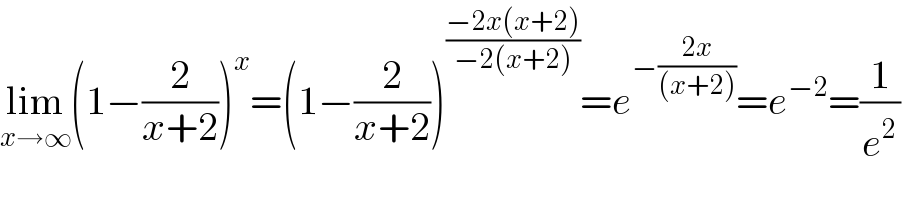
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{2}}{{x}+\mathrm{2}}\right)^{{x}} =\left(\mathrm{1}−\frac{\mathrm{2}}{{x}+\mathrm{2}}\right)^{\frac{−\mathrm{2}{x}\left({x}+\mathrm{2}\right)}{−\mathrm{2}\left({x}+\mathrm{2}\right)}} ={e}^{−\frac{\mathrm{2}{x}}{\left({x}+\mathrm{2}\right)}} ={e}^{−\mathrm{2}} =\frac{\mathrm{1}}{{e}^{\mathrm{2}} } \\ $$
