
Question Number 195453 by Rodier97 last updated on 02/Aug/23
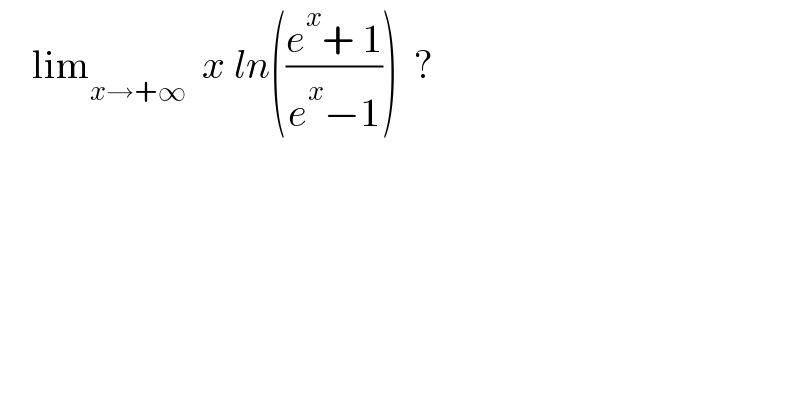
$$\:\:\:\:\mathrm{lim}_{{x}\rightarrow+\infty\:\:} \:{x}\:{ln}\left(\frac{{e}^{{x}} +\:\mathrm{1}}{{e}^{{x}} −\mathrm{1}}\right)\:\:? \\ $$
Commented by Frix last updated on 02/Aug/23

$$\mathrm{0} \\ $$
Answered by MM42 last updated on 02/Aug/23
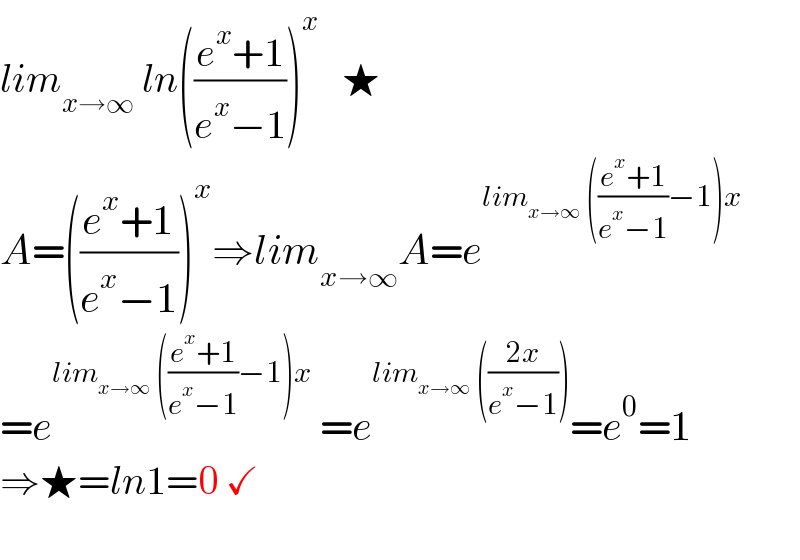
$${lim}_{{x}\rightarrow\infty} \:{ln}\left(\frac{{e}^{{x}} +\mathrm{1}}{{e}^{{x}} −\mathrm{1}}\right)^{{x}} \:\:\:\bigstar \\ $$$${A}=\left(\frac{{e}^{{x}} +\mathrm{1}}{{e}^{{x}} −\mathrm{1}}\right)^{{x}} \Rightarrow{lim}_{{x}\rightarrow\infty} {A}={e}^{{lim}_{{x}\rightarrow\infty} \:\left(\frac{{e}^{{x}} +\mathrm{1}}{{e}^{{x}} −\mathrm{1}}−\mathrm{1}\right){x}} \:\: \\ $$$$={e}^{{lim}_{{x}\rightarrow\infty} \:\left(\frac{{e}^{{x}} +\mathrm{1}}{{e}^{{x}} −\mathrm{1}}−\mathrm{1}\right){x}} \:={e}^{{lim}_{{x}\rightarrow\infty} \:\left(\frac{\mathrm{2}{x}}{{e}^{{x}} −\mathrm{1}}\right)} ={e}^{\mathrm{0}} =\mathrm{1} \\ $$$$\Rightarrow\bigstar={ln}\mathrm{1}=\mathrm{0}\:\checkmark \\ $$$$ \\ $$
