
Question Number 207339 by Ghisom last updated on 12/May/24
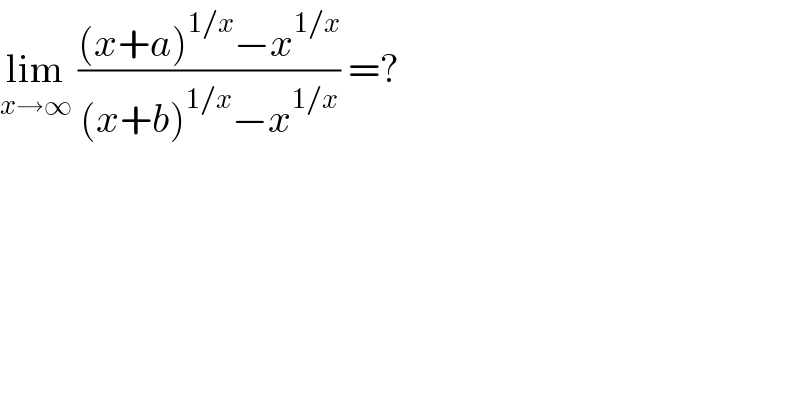
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left({x}+{a}\right)^{\mathrm{1}/{x}} −{x}^{\mathrm{1}/{x}} }{\left({x}+{b}\right)^{\mathrm{1}/{x}} −{x}^{\mathrm{1}/{x}} }\:=? \\ $$
Answered by sniper237 last updated on 12/May/24
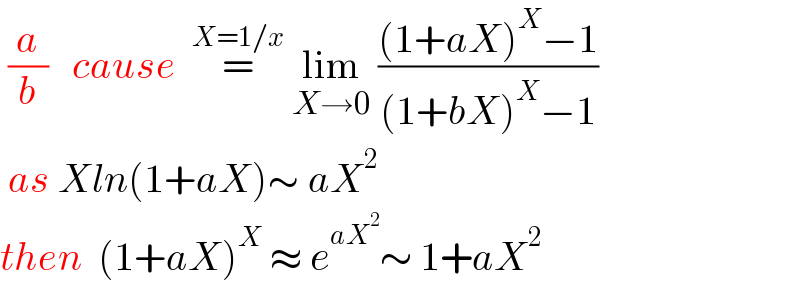
$$\:\frac{{a}}{{b}}\:\:\:{cause}\:\:\overset{{X}=\mathrm{1}/{x}} {=}\:\underset{{X}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+{aX}\right)^{{X}} −\mathrm{1}}{\left(\mathrm{1}+{bX}\right)^{{X}} −\mathrm{1}}\: \\ $$$$\:{as}\:{Xln}\left(\mathrm{1}+{aX}\right)\sim\:{aX}^{\mathrm{2}} \\ $$$${then}\:\:\left(\mathrm{1}+{aX}\right)^{{X}} \:\approx\:{e}^{{aX}^{\mathrm{2}} } \sim\:\mathrm{1}+{aX}^{\mathrm{2}} \: \\ $$
Commented by Ghisom last updated on 13/May/24

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mathzup last updated on 12/May/24
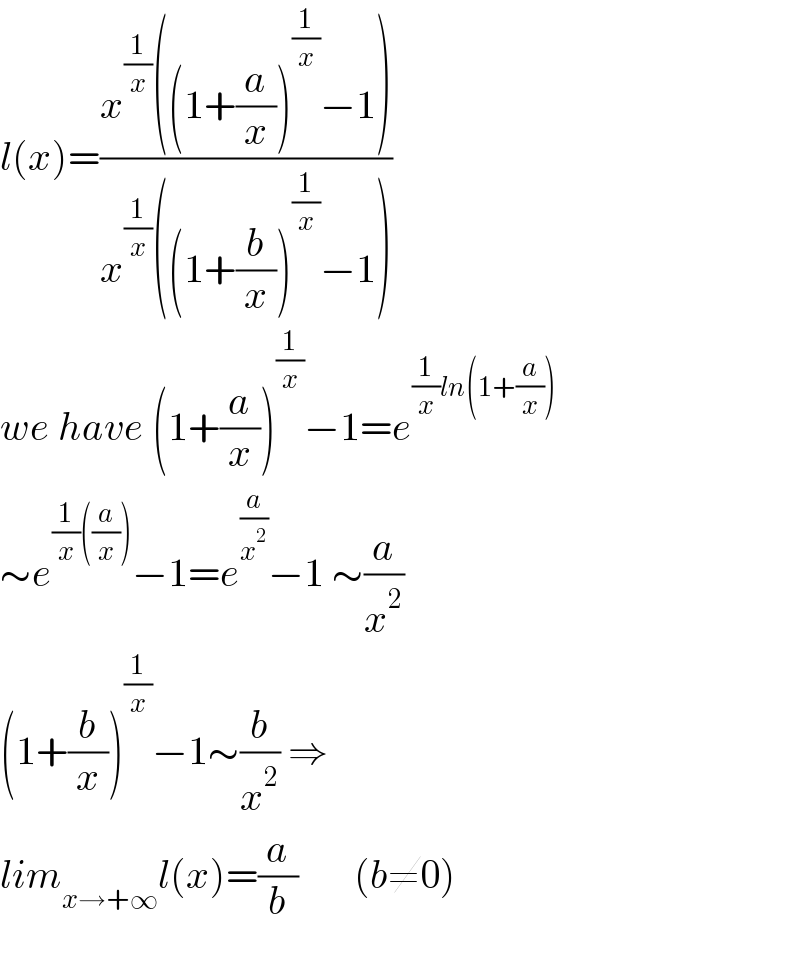
$${l}\left({x}\right)=\frac{{x}^{\frac{\mathrm{1}}{{x}}} \left(\left(\mathrm{1}+\frac{{a}}{{x}}\right)^{\frac{\mathrm{1}}{{x}}} −\mathrm{1}\right)}{{x}^{\frac{\mathrm{1}}{{x}}} \left(\left(\mathrm{1}+\frac{{b}}{{x}}\right)^{\frac{\mathrm{1}}{{x}}} −\mathrm{1}\right)} \\ $$$${we}\:{have}\:\left(\mathrm{1}+\frac{{a}}{{x}}\right)^{\frac{\mathrm{1}}{{x}}} −\mathrm{1}={e}^{\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}+\frac{{a}}{{x}}\right)} \\ $$$$\sim{e}^{\frac{\mathrm{1}}{{x}}\left(\frac{{a}}{{x}}\right)} −\mathrm{1}={e}^{\frac{{a}}{{x}^{\mathrm{2}} }} −\mathrm{1}\:\sim\frac{{a}}{{x}^{\mathrm{2}} }\: \\ $$$$\left(\mathrm{1}+\frac{{b}}{{x}}\right)^{\frac{\mathrm{1}}{{x}}} −\mathrm{1}\sim\frac{{b}}{{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} {l}\left({x}\right)=\frac{{a}}{{b}}\:\:\:\:\:\:\:\left({b}\neq\mathrm{0}\right) \\ $$$$ \\ $$
Commented by Ghisom last updated on 13/May/24

$$\mathrm{thank}\:\mathrm{you} \\ $$
