
Question Number 84873 by john santu last updated on 17/Mar/20
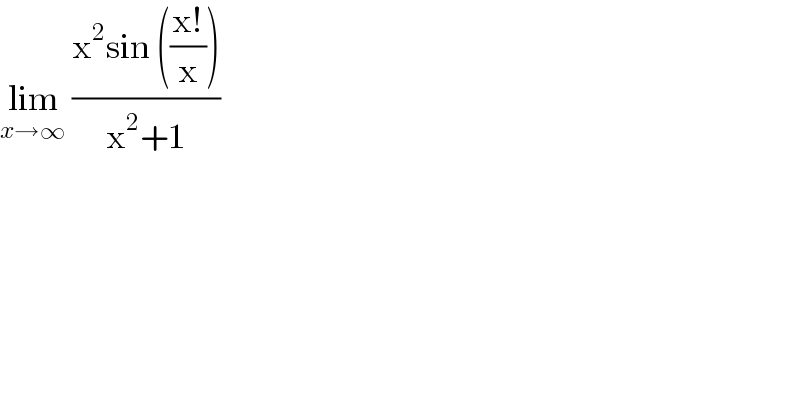
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\left(\frac{\mathrm{x}!}{\mathrm{x}}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}} \\ $$
Commented by john santu last updated on 17/Mar/20

$$\mathrm{yes}.\:\mathrm{i}\:\mathrm{agree}\:\mathrm{sir} \\ $$
Answered by bshahid010@gmail.com last updated on 17/Mar/20
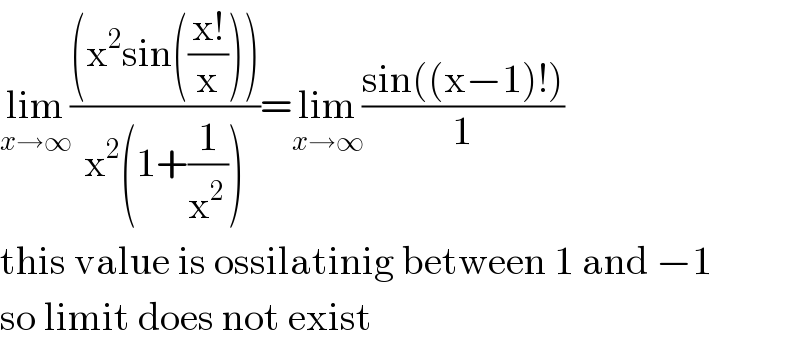
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{x}^{\mathrm{2}} \mathrm{sin}\left(\frac{\mathrm{x}!}{\mathrm{x}}\right)\right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}\:} }\right)}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{sin}\left(\left(\mathrm{x}−\mathrm{1}\right)!\right)}{\mathrm{1}} \\ $$$$\mathrm{this}\:\mathrm{value}\:\mathrm{is}\:\mathrm{ossilatinig}\:\mathrm{between}\:\mathrm{1}\:\mathrm{and}\:−\mathrm{1} \\ $$$$\mathrm{so}\:\mathrm{limit}\:\mathrm{does}\:\mathrm{not}\:\mathrm{exist} \\ $$
Answered by TANMAY PANACEA last updated on 17/Mar/20
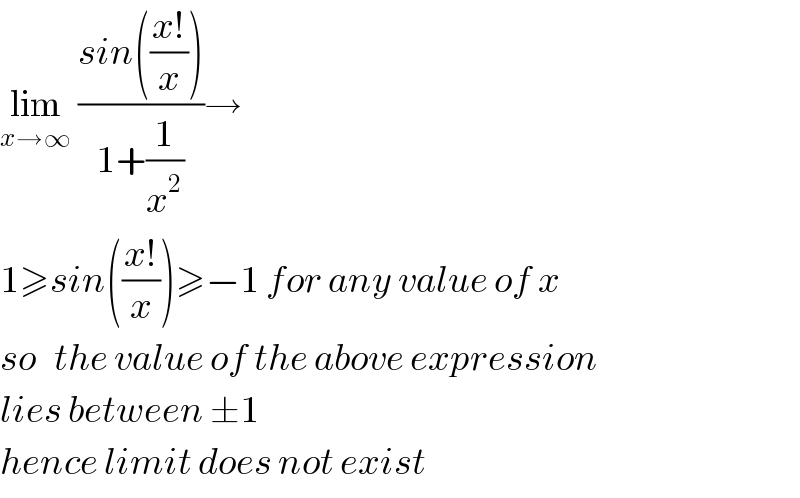
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{sin}\left(\frac{{x}!}{{x}}\right)}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\rightarrow \\ $$$$\mathrm{1}\geqslant{sin}\left(\frac{{x}!}{{x}}\right)\geqslant−\mathrm{1}\:{for}\:{any}\:{value}\:{of}\:{x} \\ $$$${so}\:\:\:{the}\:{value}\:{of}\:{the}\:{above}\:{expression}\: \\ $$$${lies}\:{between}\:\pm\mathrm{1} \\ $$$${hence}\:{limit}\:{does}\:{not}\:{exist} \\ $$
