Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 197407 by mathlove last updated on 16/Sep/23

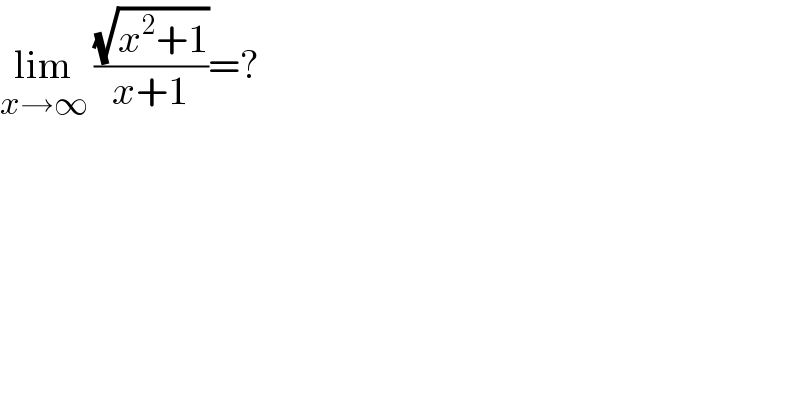
lim_(x→∞) ((√(x^2 +1))/(x+1))=?

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\mathrm{1}}=? \\ $$

Answered by Rasheed.Sindhi last updated on 16/Sep/23

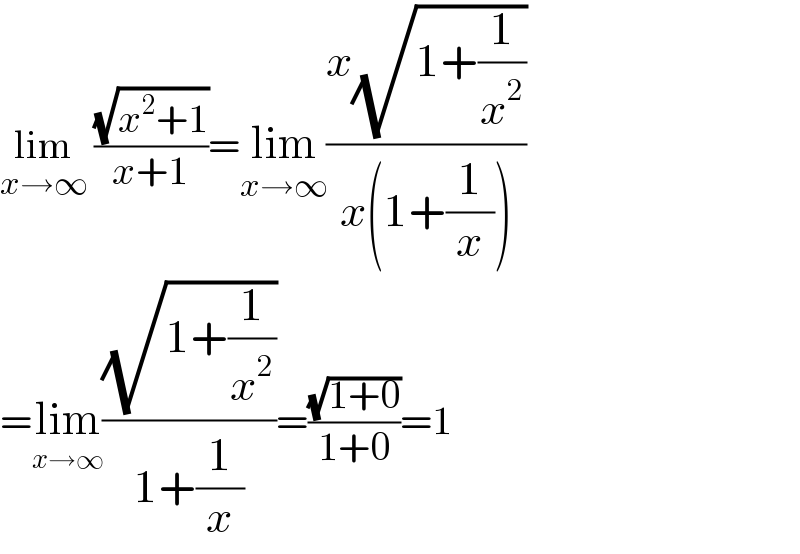
lim_(x→∞) ((√(x^2 +1))/(x+1))=lim_(x→∞) ((x(√(1+(1/x^2 ))))/(x(1+(1/x)))) =lim_(x→∞) ((√(1+(1/x^2 )))/(1+(1/x)))=((√(1+0))/(1+0))=1

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\mathrm{1}}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}{{x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}{\mathrm{1}+\frac{\mathrm{1}}{{x}}}=\frac{\sqrt{\mathrm{1}+\mathrm{0}}}{\mathrm{1}+\mathrm{0}}=\mathrm{1} \\ $$

Commented by mathlove last updated on 16/Sep/23

thanks

$${thanks} \\ $$

Answered by MM42 last updated on 16/Sep/23

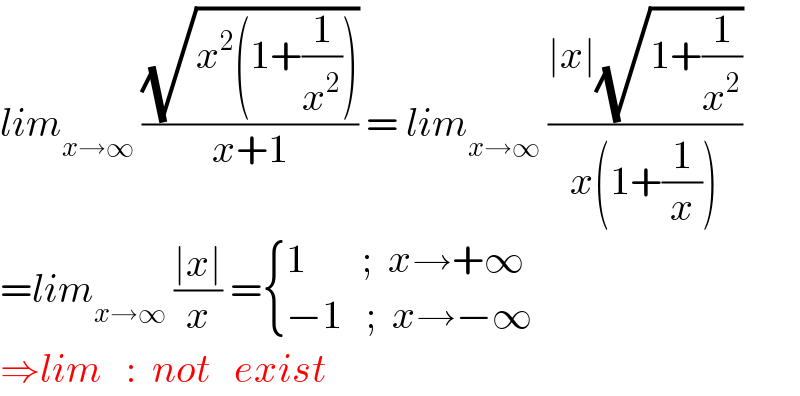
lim_(x→∞) ((√(x^2 (1+(1/x^2 ))))/(x+1)) = lim_(x→∞) ((∣x∣(√(1+(1/x^2 ))))/(x(1+(1/x)))) =lim_(x→∞) ((∣x∣)/x) = { ((1 ; x→+∞)),((−1 ; x→−∞)) :} ⇒lim : not exist

$${lim}_{{x}\rightarrow\infty} \:\frac{\sqrt{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}}{{x}+\mathrm{1}}\:=\:{lim}_{{x}\rightarrow\infty} \:\frac{\mid{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}{{x}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)}\: \\ $$$$={lim}_{{x}\rightarrow\infty} \:\frac{\mid{x}\mid}{{x}}\:=\begin{cases}{\mathrm{1}\:\:\:\:\:\:\:;\:\:{x}\rightarrow+\infty}\\{−\mathrm{1}\:\:\:;\:\:{x}\rightarrow−\infty}\end{cases} \\ $$$$\Rightarrow{lim}\:\:\::\:\:{not}\:\:\:{exist} \\ $$

Commented by MathematicalUser2357 last updated on 17/Sep/23

So lim_(x→∞) ((∣x∣)/x)≠1

$$\mathrm{So}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mid{x}\mid}{{x}}\neq\mathrm{1} \\ $$

Commented by MM42 last updated on 18/Sep/23

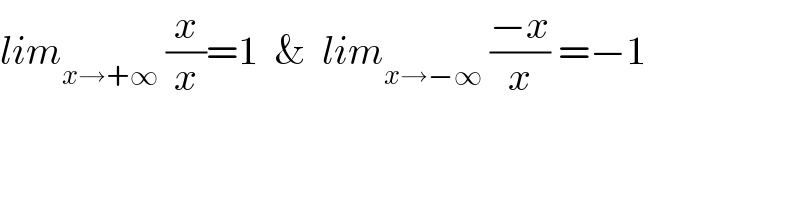
lim_(x→+∞) (x/x)=1 & lim_(x→−∞) ((−x)/x) =−1

$${lim}_{{x}\rightarrow+\infty} \:\frac{{x}}{{x}}=\mathrm{1}\:\:\&\:\:{lim}_{{x}\rightarrow−\infty} \:\frac{−{x}}{{x}}\:=−\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com