Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 179366 by mathlove last updated on 28/Oct/22

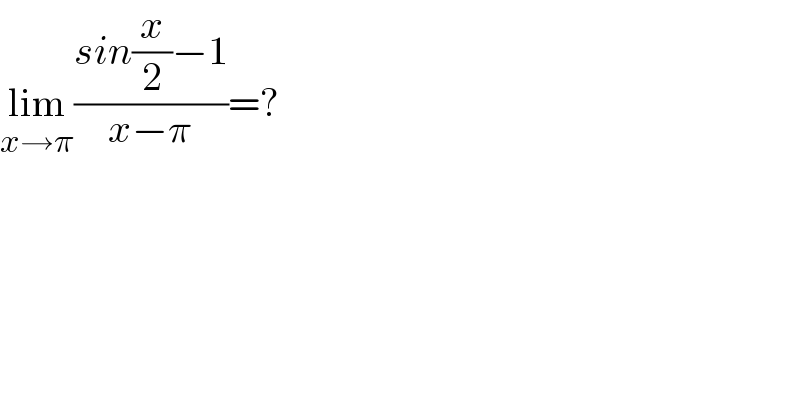
lim_(x→π) ((sin(x/2)−1)/(x−π))=?

$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{{sin}\frac{{x}}{\mathrm{2}}−\mathrm{1}}{{x}−\pi}=? \\ $$

Commented by mahdipoor last updated on 28/Oct/22

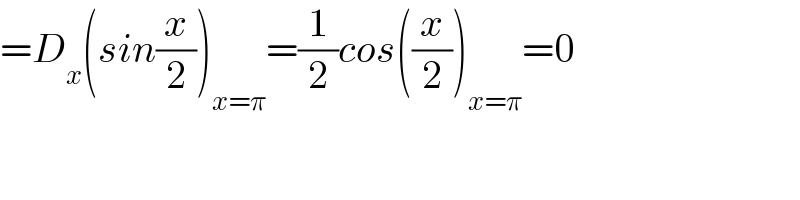
=D_x (sin(x/2))_(x=π) =(1/2)cos((x/2))_(x=π) =0

$$={D}_{{x}} \left({sin}\frac{{x}}{\mathrm{2}}\right)_{{x}=\pi} =\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\frac{{x}}{\mathrm{2}}\right)_{{x}=\pi} =\mathrm{0} \\ $$

Commented by mathlove last updated on 28/Oct/22

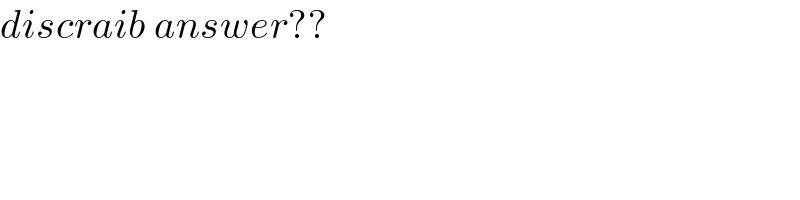
discraib answer??

$${discraib}\:{answer}?? \\ $$

Commented by mr W last updated on 29/Oct/22

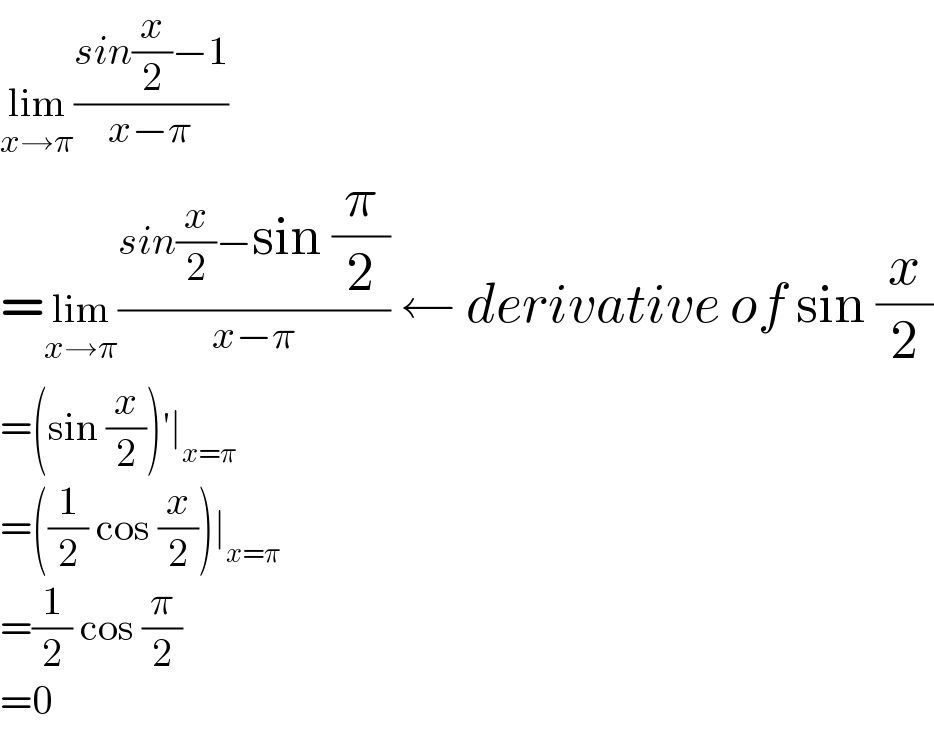
lim_(x→π) ((sin(x/2)−1)/(x−π)) =lim_(x→π) ((sin(x/2)−sin (π/2))/(x−π)) ← derivative of sin (x/2) =(sin (x/2))′∣_(x=π) =((1/2) cos (x/2))∣_(x=π) =(1/2) cos (π/2) =0

$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{{sin}\frac{{x}}{\mathrm{2}}−\mathrm{1}}{{x}−\pi} \\ $$$$=\underset{{x}\rightarrow\pi} {\mathrm{lim}}\frac{{sin}\frac{{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\pi}{\mathrm{2}}}{{x}−\pi}\:\leftarrow\:{derivative}\:{of}\:\mathrm{sin}\:\frac{{x}}{\mathrm{2}} \\ $$$$=\left(\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)'\mid_{{x}=\pi} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\right)\mid_{{x}=\pi} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}} \\ $$$$=\mathrm{0} \\ $$

Commented by mathlove last updated on 29/Oct/22

tanks

$${tanks} \\ $$

Commented by CElcedricjunior last updated on 29/Oct/22

lim_(x→𝛑) ((sin(x/2)−1)/(x−𝛑))=(0/0)=FI to apply hospital ⇔lim_(x→𝛑) ((sin(x/2)−1)/(x−𝛑))=lim_(x→𝛑) (((1/2)cos(x/2))/1)=0 lim_(x→𝛑) ((sin(x/2)−1)/(x−𝛑))=0 ...........le celebre cedric jinior......

$$\underset{{x}\rightarrow\boldsymbol{\pi}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}−\mathrm{1}}{\boldsymbol{\mathrm{x}}−\boldsymbol{\pi}}=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{\mathrm{FI}} \\ $$$$\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{apply}}\:\boldsymbol{\mathrm{hospital}}\: \\ $$$$\Leftrightarrow\underset{{x}\rightarrow\boldsymbol{\pi}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}−\mathrm{1}}{\boldsymbol{\mathrm{x}}−\boldsymbol{\pi}}=\underset{{x}\rightarrow\boldsymbol{\pi}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}}{\mathrm{1}}=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\boldsymbol{\pi}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}−\mathrm{1}}{\boldsymbol{\mathrm{x}}−\boldsymbol{\pi}}=\mathrm{0} \\ $$$$...........{le}\:{celebre}\:{cedric}\:{jinior}...... \\ $$

Answered by a.lgnaoui last updated on 28/Oct/22

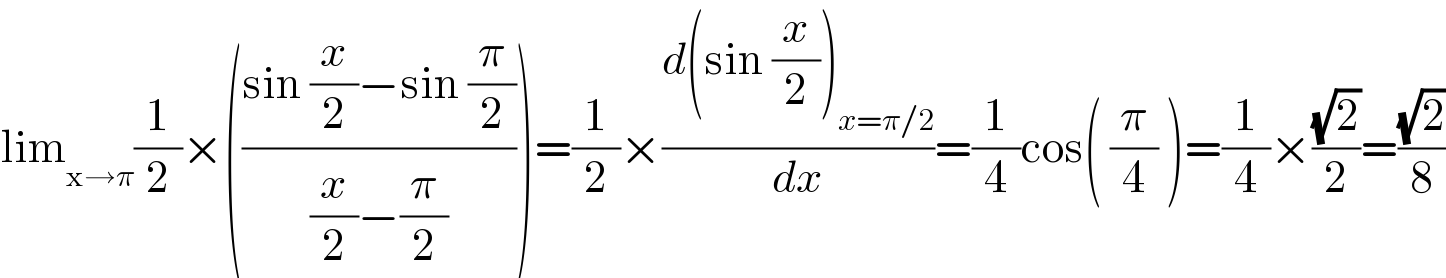
lim_(x→π) (1/2)×(((sin (x/2)−sin (π/2))/((x/2)−(π/2))))=(1/2)×((d(sin (x/2))_(x=π/2) )/dx)=(1/4)cos( (π/4) )=(1/4)×((√2)/2)=((√2)/8)

$$\mathrm{lim}_{\mathrm{x}\rightarrow\pi} \frac{\mathrm{1}}{\mathrm{2}}×\left(\frac{\mathrm{sin}\:\frac{{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\pi}{\mathrm{2}}}{\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\frac{{d}\left(\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)_{{x}=\pi/\mathrm{2}} }{{dx}}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\left(\:\frac{\pi}{\mathrm{4}}\:\right)=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$

Commented by Acem last updated on 29/Oct/22

fix (sin θ)′

$${fix}\:\left(\mathrm{sin}\:\theta\right)' \\ $$

Answered by cortano1 last updated on 29/Oct/22

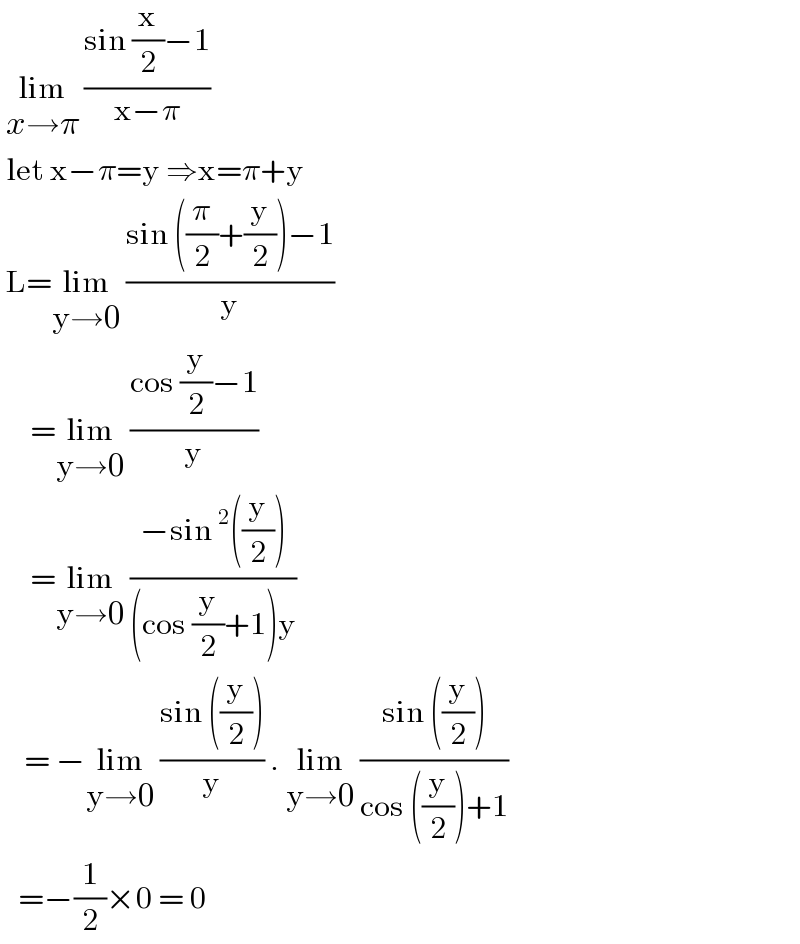
lim_(x→π) ((sin (x/2)−1)/(x−π)) let x−π=y ⇒x=π+y L=lim_(y→0) ((sin ((π/2)+(y/2))−1)/y) =lim_(y→0) ((cos (y/2)−1)/y) =lim_(y→0) ((−sin^2 ((y/2)))/((cos (y/2)+1)y)) = −lim_(y→0) ((sin ((y/2)))/y) . lim_(y→0) ((sin ((y/2)))/(cos ((y/2))+1)) =−(1/2)×0 = 0

$$\:\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{1}}{\mathrm{x}−\pi}\: \\ $$$$\:\mathrm{let}\:\mathrm{x}−\pi=\mathrm{y}\:\Rightarrow\mathrm{x}=\pi+\mathrm{y} \\ $$$$\:\mathrm{L}=\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\frac{\mathrm{y}}{\mathrm{2}}\right)−\mathrm{1}}{\mathrm{y}} \\ $$$$\:\:\:\:\:=\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\frac{\mathrm{y}}{\mathrm{2}}−\mathrm{1}}{\mathrm{y}} \\ $$$$\:\:\:\:\:=\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{y}}{\mathrm{2}}\right)}{\left(\mathrm{cos}\:\frac{\mathrm{y}}{\mathrm{2}}+\mathrm{1}\right)\mathrm{y}} \\ $$$$\:\:\:\:=\:−\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\frac{\mathrm{y}}{\mathrm{2}}\right)}{\mathrm{y}}\:.\:\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\frac{\mathrm{y}}{\mathrm{2}}\right)}{\mathrm{cos}\:\left(\frac{\mathrm{y}}{\mathrm{2}}\right)+\mathrm{1}} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{0}\:=\:\mathrm{0} \\ $$

Commented by mathlove last updated on 29/Oct/22

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com