Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 198572 by cortano12 last updated on 22/Oct/23

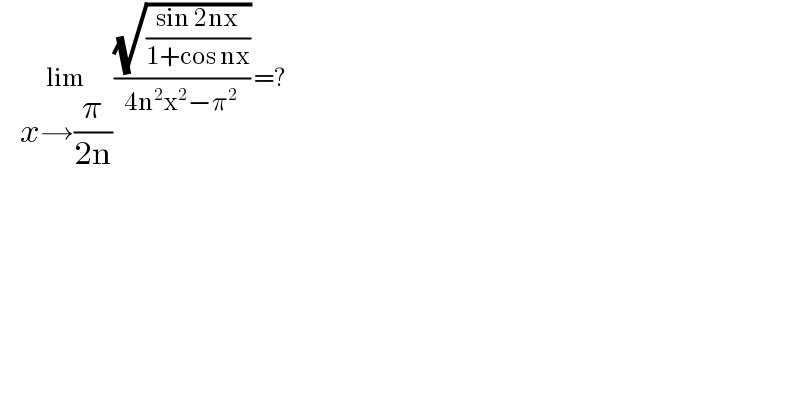
lim_(x→(π/(2n))) ((√((sin 2nx)/(1+cos nx)))/(4n^2 x^2 −π^2 )) =?

$$\:\:\:\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2n}}} {\mathrm{lim}}\:\frac{\sqrt{\frac{\mathrm{sin}\:\mathrm{2nx}}{\mathrm{1}+\mathrm{cos}\:\mathrm{nx}}}}{\mathrm{4n}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\pi^{\mathrm{2}} }\:=? \\ $$

Answered by MM42 last updated on 22/Oct/23

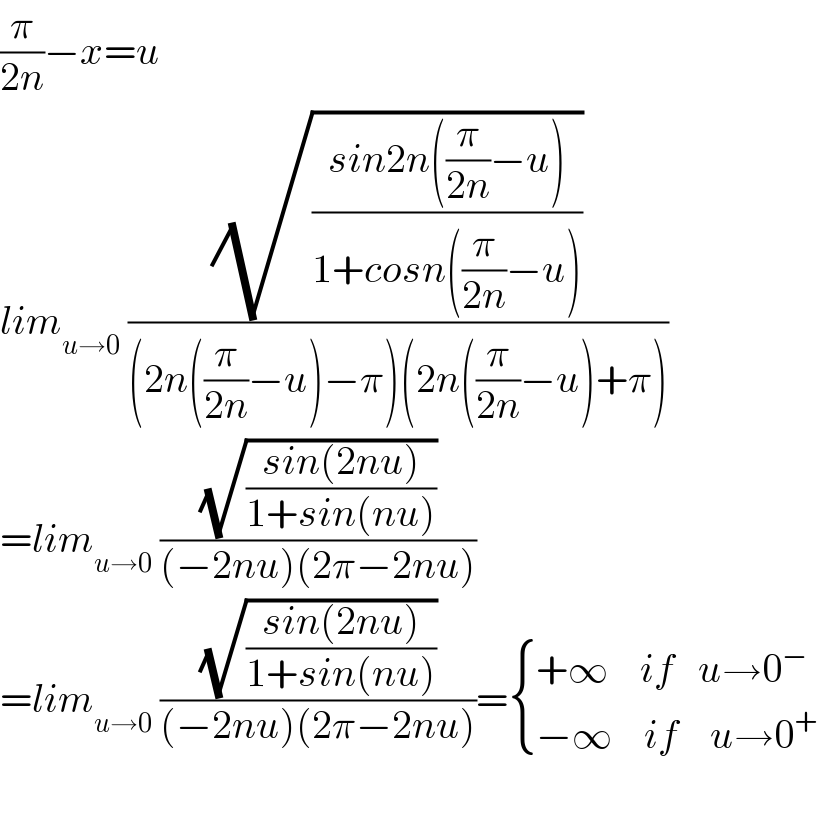
(π/(2n))−x=u lim_(u→0) ((√((sin2n((π/(2n))−u))/(1+cosn((π/(2n))−u))))/((2n((π/(2n))−u)−π)(2n((π/(2n))−u)+π))) =lim_(u→0) ((√((sin(2nu))/(1+sin(nu))))/((−2nu)(2π−2nu))) =lim_(u→0) ((√((sin(2nu))/(1+sin(nu))))/((−2nu)(2π−2nu)))= { ((+∞ if u→0^− )),((−∞ if u→0^+ )) :}

$$\frac{\pi}{\mathrm{2}{n}}−{x}={u} \\ $$$${lim}_{{u}\rightarrow\mathrm{0}} \:\frac{\sqrt{\frac{{sin}\mathrm{2}{n}\left(\frac{\pi}{\mathrm{2}{n}}−{u}\right)}{\mathrm{1}+{cosn}\left(\frac{\pi}{\mathrm{2}{n}}−{u}\right)}}}{\left(\mathrm{2}{n}\left(\frac{\pi}{\mathrm{2}{n}}−{u}\right)−\pi\right)\left(\mathrm{2}{n}\left(\frac{\pi}{\mathrm{2}{n}}−{u}\right)+\pi\right)} \\ $$$$={lim}_{{u}\rightarrow\mathrm{0}} \:\frac{\sqrt{\frac{{sin}\left(\mathrm{2}{nu}\right)}{\mathrm{1}+{sin}\left({nu}\right)}}}{\left(−\mathrm{2}{nu}\right)\left(\mathrm{2}\pi−\mathrm{2}{nu}\right)} \\ $$$$={lim}_{{u}\rightarrow\mathrm{0}} \:\frac{\sqrt{\frac{{sin}\left(\mathrm{2}{nu}\right)}{\mathrm{1}+{sin}\left({nu}\right)}}}{\left(−\mathrm{2}{nu}\right)\left(\mathrm{2}\pi−\mathrm{2}{nu}\right)}=\begin{cases}{+\infty\:\:\:\:{if}\:\:\:{u}\rightarrow\mathrm{0}^{−} }\\{−\infty\:\:\:\:{if}\:\:\:\:{u}\rightarrow\mathrm{0}^{+} }\end{cases} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com