Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 138996 by bramlexs22 last updated on 21/Apr/21

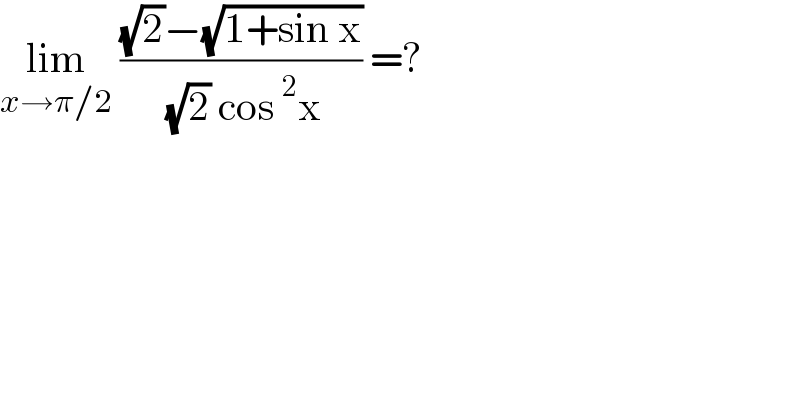
lim_(x→π/2) (((√2)−(√(1+sin x)))/( (√2) cos^2 x)) =?

$$\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}}{\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:=? \\ $$$$ \\ $$

Answered by EDWIN88 last updated on 21/Apr/21

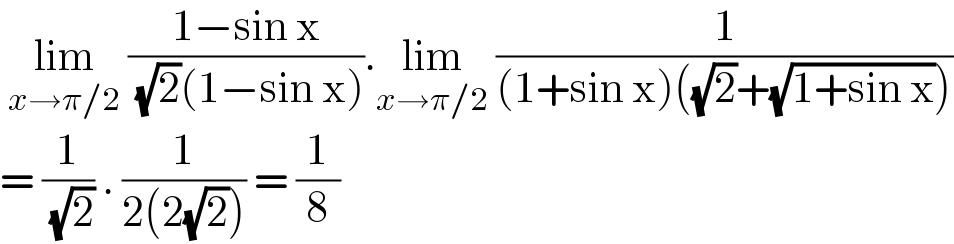
lim_(x→π/2) ((1−sin x)/( (√2)(1−sin x))).lim_(x→π/2) (1/((1+sin x)((√2)+(√(1+sin x))))) = (1/( (√2))) . (1/(2(2(√2)))) = (1/8)

$$\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}{\:\sqrt{\mathrm{2}}\left(\mathrm{1}−\mathrm{sin}\:\mathrm{x}\right)}.\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right)\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:.\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}\sqrt{\mathrm{2}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$

Answered by mathmax by abdo last updated on 22/Apr/21

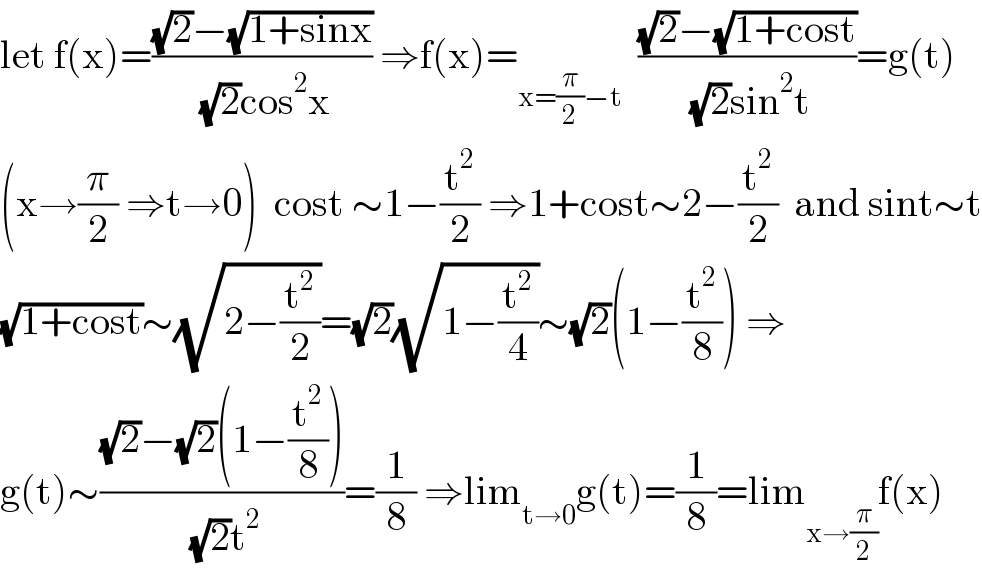
let f(x)=(((√2)−(√(1+sinx)))/( (√2)cos^2 x)) ⇒f(x)=_(x=(π/2)−t) (((√2)−(√(1+cost)))/( (√2)sin^2 t))=g(t) (x→(π/2) ⇒t→0) cost ∼1−(t^2 /2) ⇒1+cost∼2−(t^2 /2) and sint∼t (√(1+cost))∼(√(2−(t^2 /2)))=(√2)(√(1−(t^2 /4)))∼(√2)(1−(t^2 /8)) ⇒ g(t)∼(((√2)−(√2)(1−(t^2 /8)))/( (√2)t^2 ))=(1/8) ⇒lim_(t→0) g(t)=(1/8)=lim_(x→(π/2)) f(x)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}+\mathrm{sinx}}}{\:\sqrt{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=_{\mathrm{x}=\frac{\pi}{\mathrm{2}}−\mathrm{t}} \:\:\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}+\mathrm{cost}}}{\:\sqrt{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \mathrm{t}}=\mathrm{g}\left(\mathrm{t}\right) \\ $$$$\left(\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\right)\:\:\mathrm{cost}\:\sim\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{1}+\mathrm{cost}\sim\mathrm{2}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:\:\mathrm{and}\:\mathrm{sint}\sim\mathrm{t} \\ $$$$\sqrt{\mathrm{1}+\mathrm{cost}}\sim\sqrt{\mathrm{2}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}}=\sqrt{\mathrm{2}}\sqrt{\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}}}\sim\sqrt{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{8}}\right)\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{t}\right)\sim\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{8}}\right)}{\:\sqrt{\mathrm{2}}\mathrm{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{8}}=\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} \mathrm{f}\left(\mathrm{x}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com