
Question Number 129655 by liberty last updated on 17/Jan/21
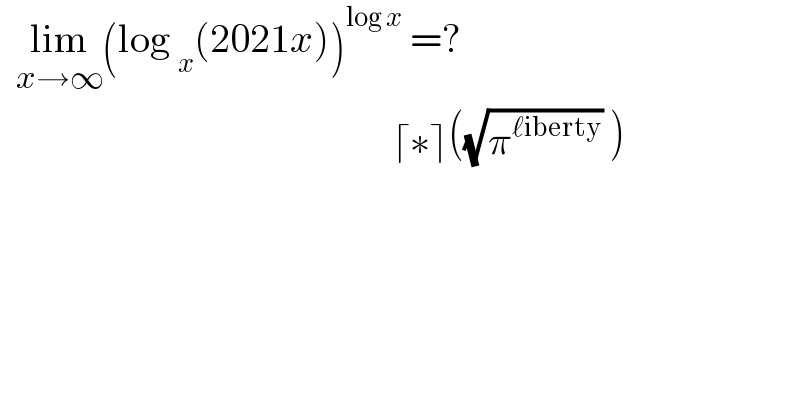
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{log}\:_{{x}} \left(\mathrm{2021}{x}\right)\right)^{\mathrm{log}\:{x}} \:=? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\lceil\ast\rceil\left(\sqrt{\pi^{\ell\mathrm{iberty}} }\:\right) \\ $$
Answered by bemath last updated on 17/Jan/21
![lim_(x→∞) (((ln (2021x))/(ln x)))^(ln x) = lim_(x→∞) (1+((ln 2021)/(ln x)))^(ln x) lim_(x→∞) [(1+(1/((((ln x)/(ln 2021))))))((ln x)/(ln 2021)) ]^(ln 2021) = e^(ln 2021) = 2021](Q129662.png)
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{ln}\:\left(\mathrm{2021x}\right)}{\mathrm{ln}\:\mathrm{x}}\right)^{\mathrm{ln}\:\mathrm{x}} =\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{ln}\:\mathrm{2021}}{\mathrm{ln}\:\mathrm{x}}\right)^{\mathrm{ln}\:\mathrm{x}} \\ $$$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{\left(\frac{\mathrm{ln}\:\mathrm{x}}{\mathrm{ln}\:\mathrm{2021}}\right)}\right)\frac{\mathrm{ln}\:\mathrm{x}}{\mathrm{ln}\:\mathrm{2021}}\:\right]^{\mathrm{ln}\:\mathrm{2021}} =\:\mathrm{e}^{\mathrm{ln}\:\mathrm{2021}} \:=\:\mathrm{2021} \\ $$
