
Question Number 72495 by Tony Lin last updated on 29/Oct/19
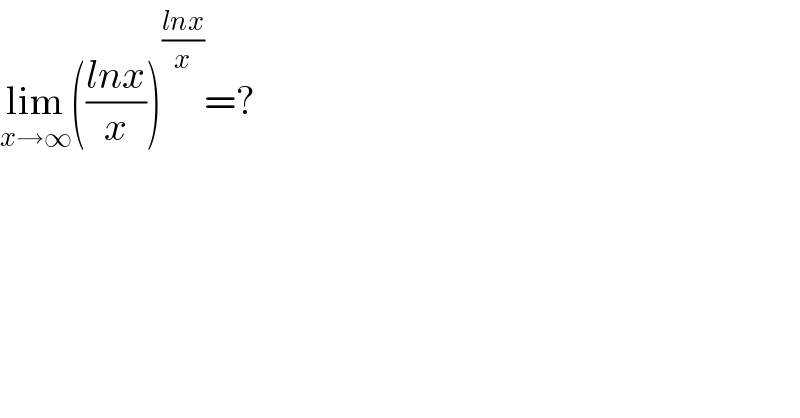
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{lnx}}{{x}}\right)^{\frac{{lnx}}{{x}}} =? \\ $$
Commented by mathmax by abdo last updated on 29/Oct/19
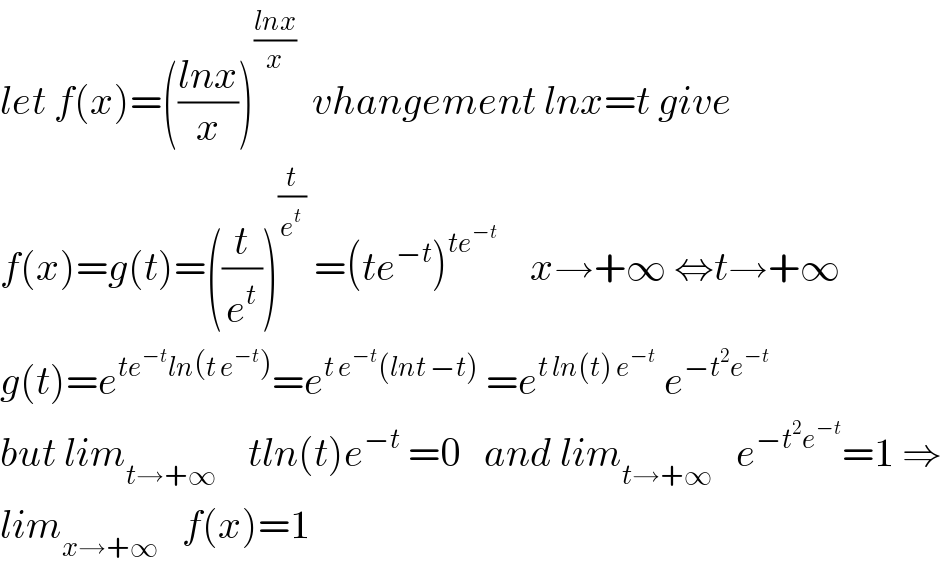
$${let}\:{f}\left({x}\right)=\left(\frac{{lnx}}{{x}}\right)^{\frac{{lnx}}{{x}}} \:\:{vhangement}\:{lnx}={t}\:{give}\: \\ $$$${f}\left({x}\right)={g}\left({t}\right)=\left(\frac{{t}}{{e}^{{t}} }\right)^{\frac{{t}}{{e}^{{t}} }} \:=\left({te}^{−{t}} \right)^{{te}^{−{t}} } \:\:\:\:{x}\rightarrow+\infty\:\Leftrightarrow{t}\rightarrow+\infty \\ $$$${g}\left({t}\right)={e}^{{te}^{−{t}} {ln}\left({t}\:{e}^{−{t}} \right)} ={e}^{{t}\:{e}^{−{t}} \left({lnt}\:−{t}\right)} \:={e}^{{t}\:{ln}\left({t}\right)\:{e}^{−{t}} } \:{e}^{−{t}^{\mathrm{2}} {e}^{−{t}} } \\ $$$${but}\:{lim}_{{t}\rightarrow+\infty} \:\:\:\:{tln}\left({t}\right){e}^{−{t}} \:=\mathrm{0}\:\:\:{and}\:{lim}_{{t}\rightarrow+\infty} \:\:\:{e}^{−{t}^{\mathrm{2}} {e}^{−{t}} } =\mathrm{1}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} \:\:\:{f}\left({x}\right)=\mathrm{1} \\ $$
Commented by Tony Lin last updated on 30/Oct/19

$${thanks}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 30/Oct/19
$${you}\:{are}\:{welcome}. \\ $$
