
Question Number 193262 by josemate19 last updated on 09/Jun/23
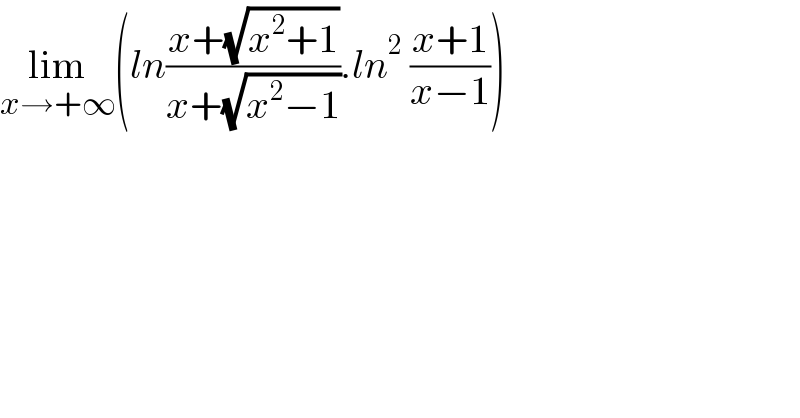
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\left({ln}\frac{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}.{ln}^{\mathrm{2}} \:\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right) \\ $$$$ \\ $$
Answered by qaz last updated on 09/Jun/23
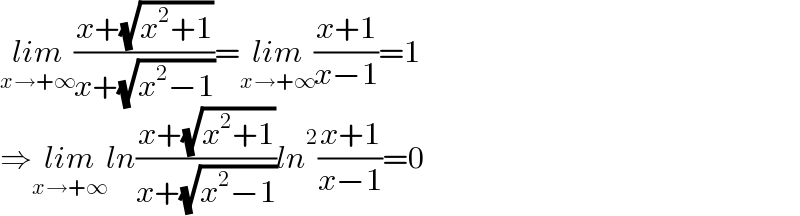
$$\underset{{x}\rightarrow+\infty} {{lim}}\frac{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}=\underset{{x}\rightarrow+\infty} {{lim}}\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}=\mathrm{1} \\ $$$$\Rightarrow\underset{{x}\rightarrow+\infty} {{lim}ln}\frac{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{ln}^{\mathrm{2}} \frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}=\mathrm{0} \\ $$
