
Question Number 175994 by sciencestudent last updated on 10/Sep/22
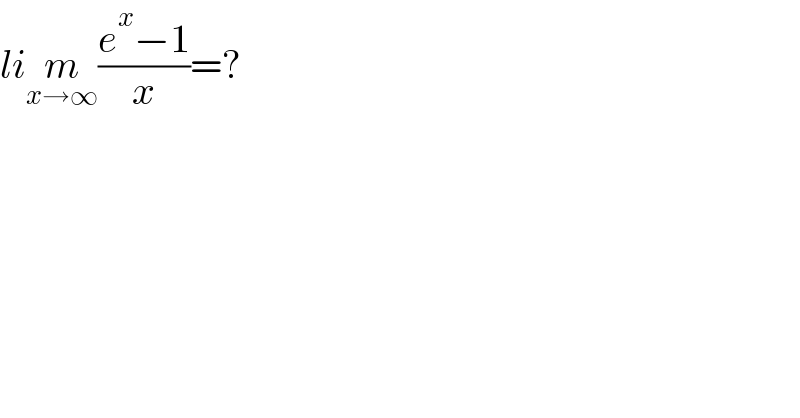
$${li}\underset{{x}\rightarrow\infty} {{m}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}=? \\ $$
Answered by JDamian last updated on 10/Sep/22

$$\infty \\ $$
Answered by cortano2 last updated on 11/Sep/22

$$=\frac{{e}^{\infty} −\mathrm{1}}{\infty}=\frac{\infty}{\infty}=\mathrm{1} \\ $$
Commented by Ar Brandon last updated on 11/Sep/22
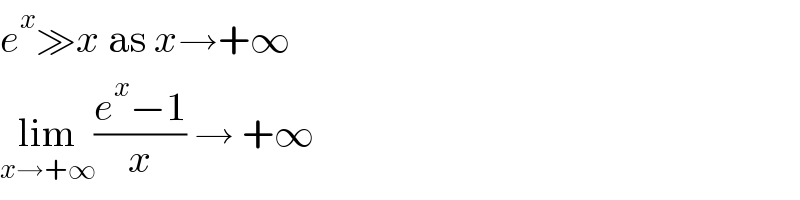
$${e}^{{x}} \gg{x}\:\mathrm{as}\:{x}\rightarrow+\infty \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}\:\rightarrow\:+\infty \\ $$
Answered by Raxreedoroid last updated on 11/Sep/22

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}\left(\frac{\infty}{\infty}\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{e}^{{x}} }{\mathrm{1}}=+\infty \\ $$
