
Question Number 216014 by mathlove last updated on 25/Jan/25
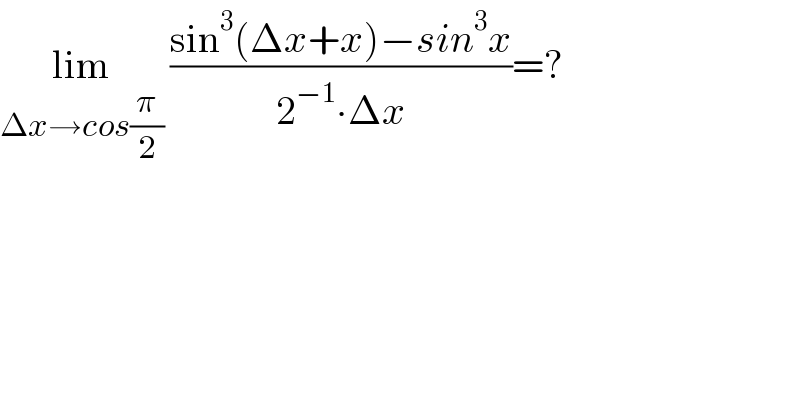
$$\underset{\Delta{x}\rightarrow{cos}\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\mathrm{sin}^{\mathrm{3}} \left(\Delta{x}+{x}\right)−{sin}^{\mathrm{3}} {x}}{\mathrm{2}^{−\mathrm{1}} \centerdot\Delta{x}}=? \\ $$
Answered by MrGaster last updated on 26/Jan/25
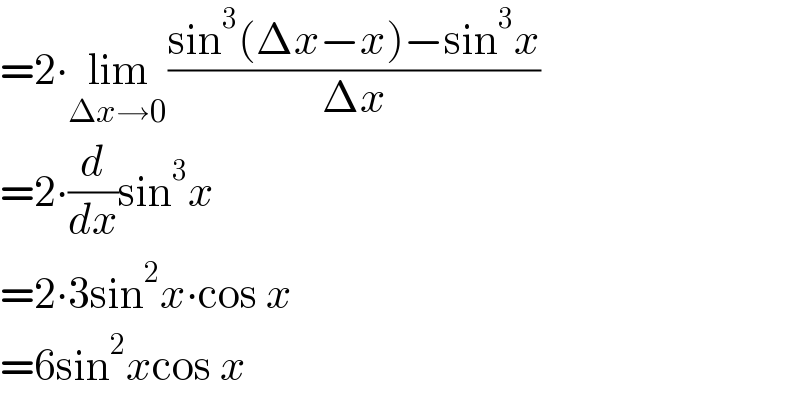
$$=\mathrm{2}\centerdot\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}^{\mathrm{3}} \left(\Delta{x}−{x}\right)−\mathrm{sin}^{\mathrm{3}} {x}}{\Delta{x}} \\ $$$$=\mathrm{2}\centerdot\frac{{d}}{{dx}}\mathrm{sin}^{\mathrm{3}} {x} \\ $$$$=\mathrm{2}\centerdot\mathrm{3sin}^{\mathrm{2}} {x}\centerdot\mathrm{cos}\:{x} \\ $$$$=\mathrm{6sin}^{\mathrm{2}} {x}\mathrm{cos}\:{x} \\ $$
